1.1 Repetition av viktig algebra
Inget nytt här, ni bör känna igen er från de tidigare kurserna. Om inte, repetera de grundläggande algebraiska reglerna.
| Khan Academy |
|---|
| Algebraic expressions |
| Quadratics and polynomials |
| Equations and geometry |
Lös uppgifter efter behov.
1.2 Trigonometri i rätvinklig triangel
Vid det här laget är ni bekanta med så kallade rätvinkliga trianglar. Ni vet också att sidorna i en sådan triangel har speciella namn, det är avgörande att ni kan särskilja dessa från och med nu.
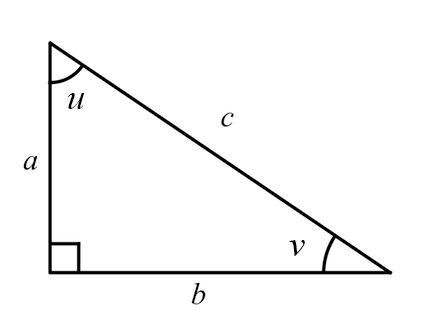 |
$\sin v =\dfrac{\textrm{motstående katet}}{\textrm{hypotenusa}}=\dfrac{a}{c}$ $\cos v =\dfrac{\textrm{närliggande katet}}{\textrm{hypotenusa}}=\dfrac{b}{c}$ $\tan v =\dfrac{\textrm{motstående katet}}{\textrm{närliggande katet}}=\dfrac{a}{b}$ $\sin u =\dfrac{\textrm{motstående katet}}{\textrm{hypotenusa}}=\dfrac{b}{c}$ $\cos u =\dfrac{\textrm{närliggande katet}}{\textrm{hypotenusa}}=\dfrac{a}{c}$ $\tan u =\dfrac{\textrm{motstående katet}}{\textrm{närliggande katet}}=\dfrac{b}{a}$ |
Lös 1201-1207 och fler efter behov.
Exakta värden (sid 14-16)
I vissa rätvinkliga trianglar kan man bestämma $\sin$, $\cos$ och $\tan$ exakt. Det handlar om likbent respektive halv liksidig triangel. Om ni tränar er på att utföra beräkningarna för att ta fram dessa exakta värden får ni också en bättre förståelse för hur begreppen hänger ihop.
| Halv kvadrat | Halv liksidig triangel |
|---|---|
enhetscirkeln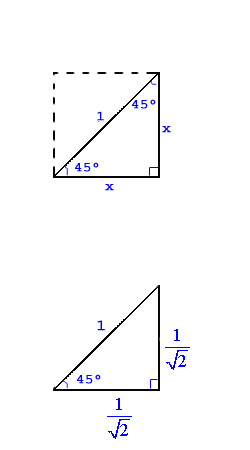 |
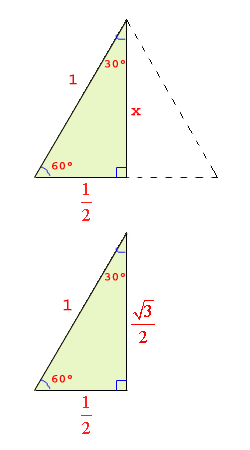 |
Lös 1218-1223, 1225,1226
1.3 Enhetscirkeln
Att förstå och kunna använda sig av enhetscirkeln är mycket användbart, både i denna kurs och framöver i era kommande matematikstudier, så ägg ner ordentligt med tid på att studera hur enhetscirkeln fungerar. Börja med att kika på GeGebra konstruktionerna nedan. Den genomgång som Malin Christersson har gjort är också utmärkt.
| GeoGebra Appar | |
|---|---|
| Ma3c-1.1 | Enhetscirkeln |
| Ma3c-1.2 | The Unit Circle med Malin C. |
OBS!!! Notera att för en vilken godlycklig vinkel $v$ som helst i enhetscirkeln bildas alltid en rätvinklig triangel där hyponeusan har längden 1 (hypotenusan är ju alltid radien i enhetscirkeln). Vidare, för rätvinkliga trianglar gäller ju Pythagoras sats, $x^2+y^2=1$ och eftersom x-värdet ges av $\cos v$ och y-värdet av $\sin v$ erhålls följande viktiga samband.
| Trigonometriska ettan |
|---|
| $\begin{align} \sin^2 v + \cos ^2 v =1 \end{align}$ |
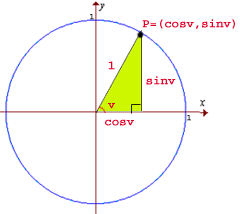 |
Säkerställ också att ni geometriskt förstår sambanden
$\sin(180^{\circ}-v)=\sin v$
$\cos(-v)=\cos v$
$\sin(-v)=-\sin v$
De två senare visar att cosinus är en jämn funktion och att sinus är en udda funktion.
Lös 1301-1309
1.4 Triangelsatserna
Nu skall vi syssla med icke-rätvinkliga trianglar och titta på några satser som kan användas.
Areasatsen (sid 22-24)
Med hjälp ac areasatsen går det att beräkna arean av en triangel om vi känner två sidor och den mellanliggande vinkeln.
| Areasatsen |
|---|
| $\begin{align} A=\dfrac{ab\sin v}{2} \end{align}$ |
 |
Lös 1401-1405.
Sinussatsen (sid 25-30)
Det finns egentligen inga genvägar för att bli bekväm och bra på att hantera trigonometriska ekvationer. Det är erfarenhet och att ha koll på trigonometriska omskrivningar som förbättrar framgångsprocenten!
Lös 1414-1421.
Cosinussatsen (sid 31-35)
Det finns egentligen inga genvägar för att bli bekväm och bra på att hantera trigonometriska ekvationer. Det är erfarenhet och att ha koll på trigonometriska omskrivningar som förbättrar framgångsprocenten!
Lös 1428-1430,1432-1433.
Det finns gott om extraövningar som ni tar er an i mån av tid och ambition.
1.5 Cirkelns ekvation
Definitionen av en cirkel lyder: En cirkel är mängden av de punkter i planet vilkas avstånd till en given punkt A är konstant och lika med $r$. Punkten A är cirkelns medelpunkt och avståndet $r$ är cirkelns radie.
| Cirkelns ekvation |
|---|
| $\left(x - a \right)^2 + \left( y - b \right)^2=r^2$ |
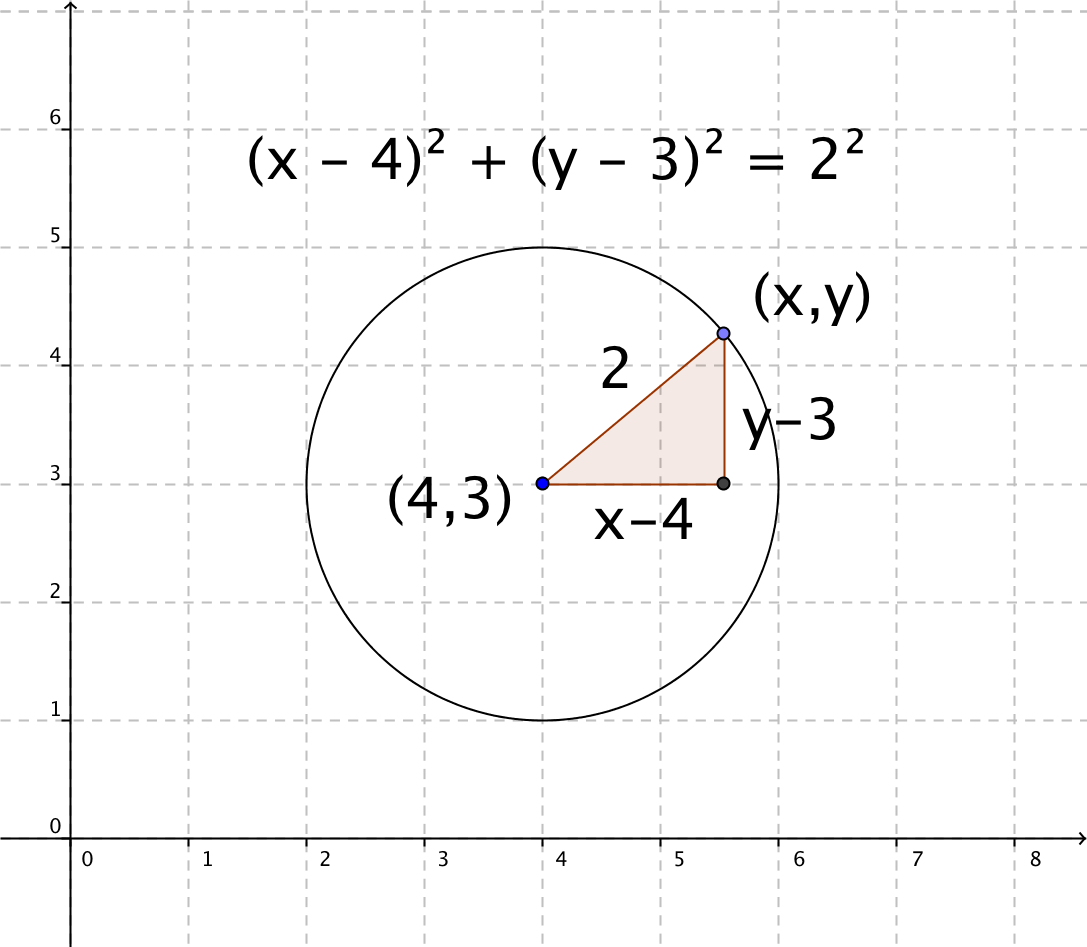 |
| Bild från wikiskola |