3.1 Bohrs modell för väteatomen

Kvanthypotesen
En atom kan bara sända ut eller ta emot energi i bestämda portioner eller kvanta.

$W=hf$, Energin ($W$) är lika med Plancks konstant ($h=6.626 \cdot 10^{-34}$) multiplicerat mer frekvensen $f$.

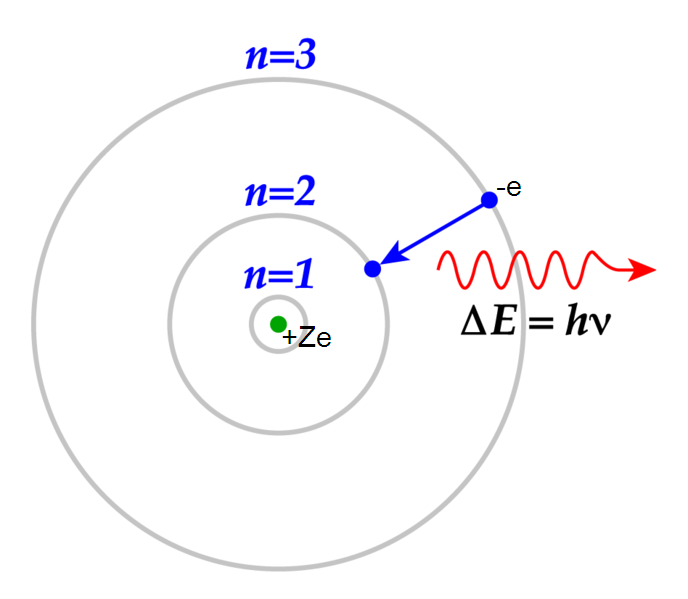
Bohrs modell av väteatomen kallas också skalmodellen, han föreställde sig en atom som bilden nedan.

Kolla även in denna korta video som visar väteatomens spektrallinjer och hur de uppkommer.

Väteatomens elektron, och alla andra atomers elektroner också för den delen, kan exciteras. Detta innebär att de tillförs ett energikvanta (en foton) med tillräckligt stor energi för att "lyfta upp" elektronen ett eller flera energisteg. Elektronerna vill hela tiden befinna sig i sitt grundtillstånd, därför kommer de nästan omedelbart att hoppa tillbaka dit och då gör de sig av med den energi som de precis fått i form av av elektromagnetisk strålning. Beroende på hur stort tillbakahoppet är, blir strålningen som den skickar ut olika energirik. Ju mer energi strålningen innehåller, desto kortare våglängd blir det.
V arje atom har sin unika uppsättning energinivåer. Nedan är vätets energinivå diagram i två olika skepnader. Negativa energinivåer därför att den joniserade väteatomen (d v s då elektronen avlägsnats) antas ha energin 0 eV.

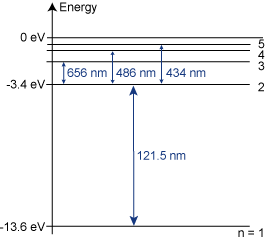
Hur kan man beräkna exempelvis våglängden på ljuset från $H_{\alpha}$ övergången? Alltså när vätets elektron faller ner från nivå 3 till nivå 2.

Genomgång av energienheten Elektronvolt eV

Se YouTubeklippet med denna beräkning.

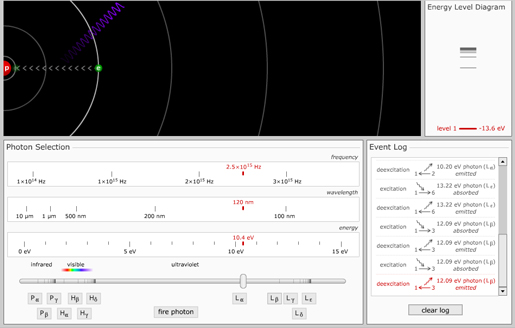
Här finns en app som simulerar väteatomens energinivåer. Genom att justera slidern kan ni bombardera elektronen med godtyckliga fotonenergier. I loggen ser ni vilka övergångar som genereras.
Försök exempelvis få fram den välkända övergången som generarar $H_{\alpha}$ linjen.

Hur bra är Bohrs modell? (sid 101)

Teorin funkar perfekt för väte och hyfsat för andra så kallade en-elektron atomer, alltså atomer med en ensam elektron (valenselektron) i ytterska skalet.

Videogenomgångar, appar och övningar
Vid.Fy2
Vid.Fy2	Från enhetscirkel till de trigonometriska funktionerna

App.Fy2
App.Fy2

Övningar	Lös 3.01, 3.02, 3.03, 3.04, 3.05, 3.06

3.2 Emission och absorbtion

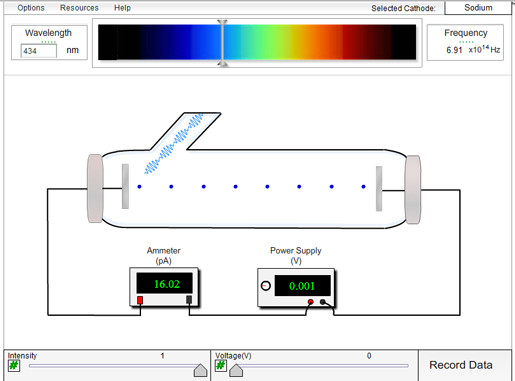
Emission av ljus från atomer och molekyler (sid 102)

Emission betyder att en atom sänder ut energi i form av en foton. Det sker alltså när en exciterad elektron faller tillbaka ner mot ett lägre energitillstånd. I bilden nedan faller elektronen ner (deexciteras) från n=3 till n=2 och en foton emiteras med den energi som skiljer de båda nivåerna åt!
Se uppgifterna 3.04 och 3.05 för exempel på hur denna energi beräknas.

Här är ett typiskt absorbtions- och emissionsspektrum från Väte.

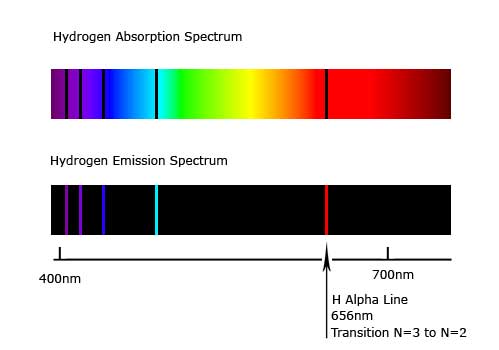
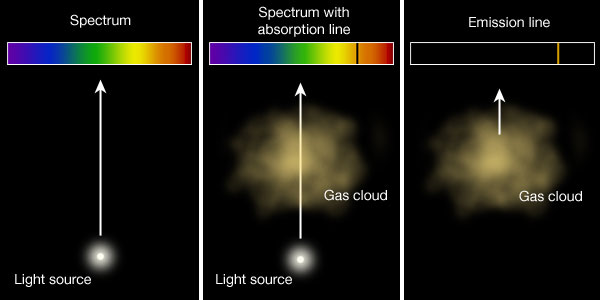
Såhär uppkommer de båda varianterna. Vid absorbtion så exciteras en viss atom av ljuset bakom gasmolnet och just den energin når inte observatören, det blir en mörk linje i spektrumet. Vid emission observeras ljuset från de deexciterade elektronerna och endast dessa.

Spektrum från molekyler (sid 103)

Spektrum från fasta ämnen (sid 104)

Emissionsspektrum från några olika atomslag.

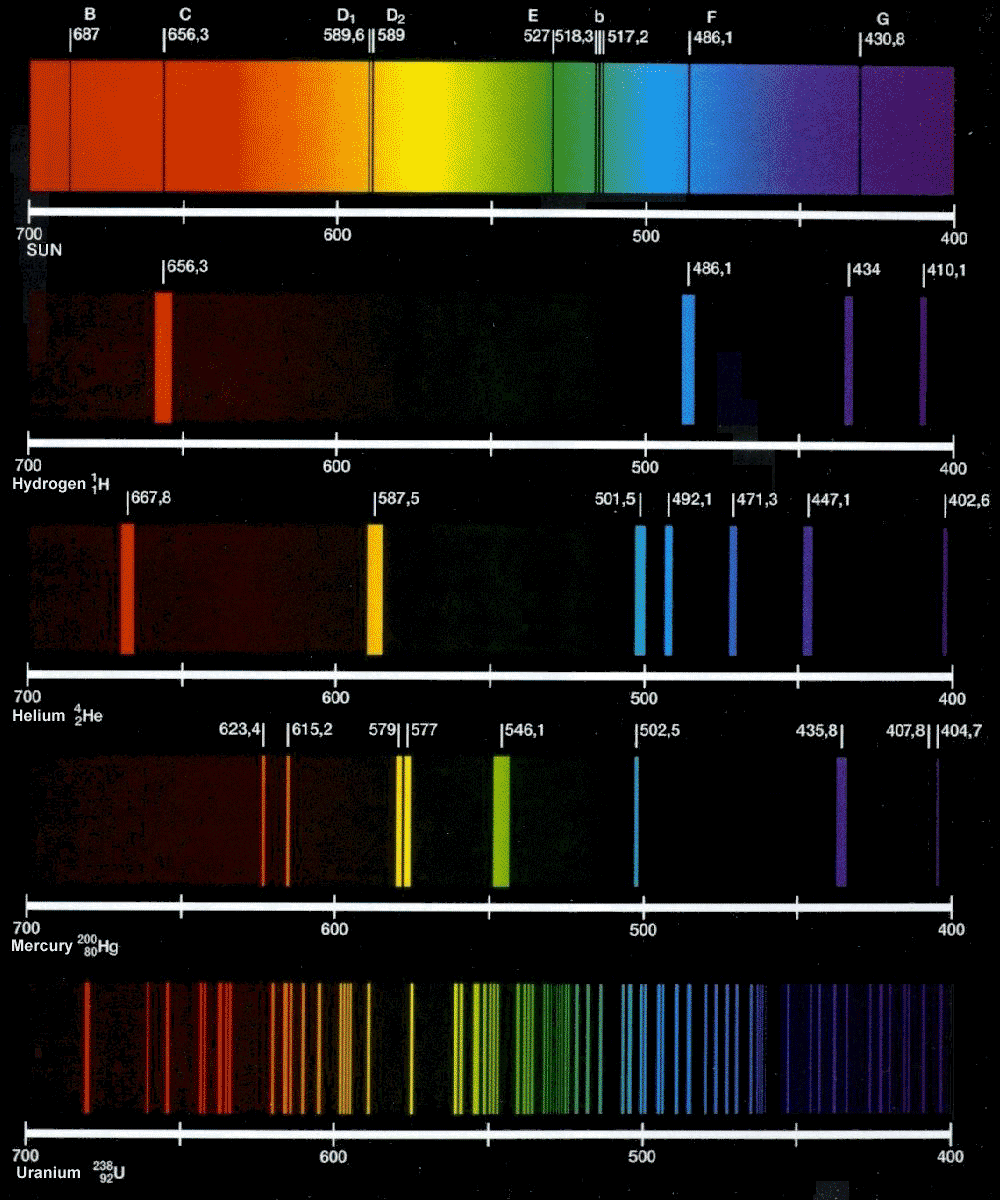
Absorption av ljus (sid 104)

Luminiscens (sid 106)

Spektret och fysikens lagar (sid 107)

Lös 3.09. 3.10, 3.11, 3.12, 3.13

3.3 Fotoelektrisk effekt

Gränsfrekvens (sid 109)

Einsteins förklaring (sid 110)

Mätning av Plancks konstant (sid 112)

Digital fotografering (sid 115)

Upplösning (sid 116)

Lös 3.15, 3.16

3.4 Fotonens rörelsemängd

Fotonen kan aldrig vara i vila och saknar således vilomassa och vi säger definitionsmässigt därför att fotonen därmed är masslös. Den har däremot en energi, en frekvens och en rörelsemängd, men begrepp som massa, storlek och läge kan inte definieras på ett meningsfullt sätt.
Fotonen har energin

$W=hf$, där $h=6.626\cdot 10^{-34}$Js är Placks konstant.

Eftersom energi och massa är ekvivalenta (via Einstens berömda formel $E=mc^2$), så har fotonen i någon mening ändå en ekvivalent massa. För alla partiklar eller objekt som har en vilomassa $m_0$ skulle det krävas en oändlig mängd energi att accelerera den till ljusets hastighet. I klassisk mening finns ingen sådan hastighetsbegränsning, rörelseenergin $E_k$ växer enligt $E_k=\dfrac{mv^2}{2}$ (den svarta kurvan nedan).

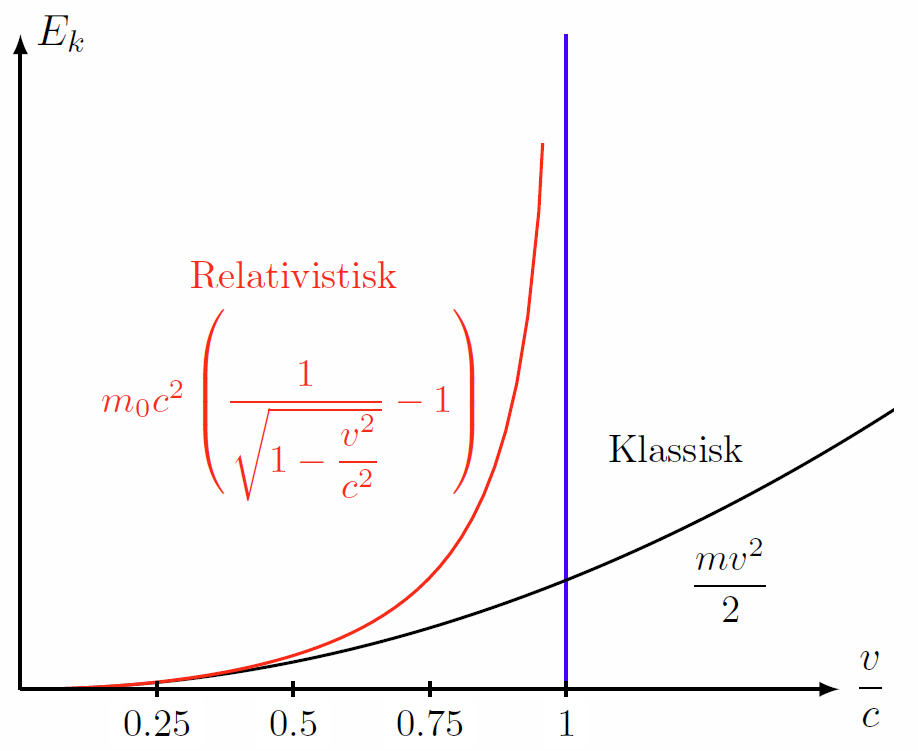
Den klassiska beskrivningen av rörelsemängd från fysik 1 kursen är att

$p=m\cdot v$

Fotonen saknar alltså vilomassa och den rör sig alltid med ljusets hastighet. Fotonens rörelsemängd $p$ blir

$p=\dfrac{E}{c}=\dfrac{hf}{c}=\dfrac{h}{\lambda}$

Lös 3.18, 3.19, 3.20

3.5 Partiklar eller vågor?

Partiklar eller vågor? (sid 121)

Louis de Broglie undrade om nu elektromagnetisk strålning, som ljus, kan vara partiklar så kanske partiklar kan vara elektromagnetisk strålning? Han undersökte om det finns en våglängd $\lambda$ till elektroner så att dess rörelsemängd kan skrivas

$p=\dfrac{h}{\lambda}$

Då $p=mv$ blir sambandet $mv=\dfrac{h}{\lambda}$, som ger våglängden för elektronen $\lambda=\dfrac{h}{mv}$. Hur stor våglängd får då en elektron med en rörelseenergi $E_k$?

$E_k=\dfrac{mv^2}{2}=\dfrac{m^2v^2}{2m} =\dfrac{p^2}{2m}$, som ger $p =\sqrt{2mE_k}$.

Elektronens våglängd blir då $\lambda= \dfrac{h}{p}= \dfrac{h}{\sqrt{2mE_k}}$.

Denna storlek på våglängden motsvarar avståndet mellan atomerna i en kristall. Detta stämmer med experiment som gjorts. Man lät en elektronstråle reflekteras mot en kristall och mätte antal elektroner som reflekterats i olika riktningar. Man fick då en maximal intensitet i de riktningar som stämde med de Broglies våglängd för elektronen.

JohanMatteFysik

Gymnasieskolan Spyken, LUND