2.1 Reflektion och brytning
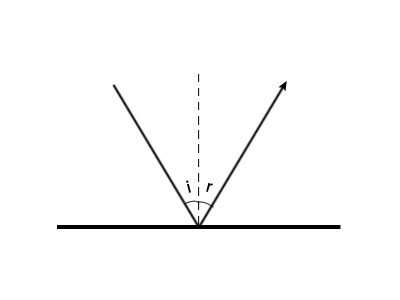
Reflektion (sid 58)
Danske astronomen Ole Römer var först med att inse att ljusets hastighet inte är oändligt hög, han lyckades också beräkna hastigheten.
Nu vet vi att ljushastigheten i vakuum är $c=299\,792\,458$ m/s.
Reflektionslagen säger att reflektionsvinkeln ($\alpha_r$) är lika med infallsvinkeln ($\alpha_i$).
$\alpha_i=\alpha_r$
Brytning (sid 59-62)
Brytning eller refraktion inträffar när ljus passerar från ett medium till ett annat. Ljuset ändrar då riktning, det bryts, och en enkel förklaring till detta är att ljuset färdas olika fort i olika medium. Ljuset följer den väg mellan två punkter som tar kortast tid. Detta kallas för Fermats Princip efter advokaten och matematikern Pierre de Fermat. Att ljus färdas olika snabbt i olika medier kan vi se som en ren materialegenskap. Detta sammanfattas i begreppet brytningsindex ($n$), vilket är förhållandet mellan ljushastigheten i vakuum ($c$) och ljushastigheten i mediet ($v$).
$ n=\dfrac{c}{v}$
Brytningslagen eller som den också kallas Snell's lag
$ n_1\sin \alpha_1=n_2 \sin \alpha_2$
gäller när en ljusstråle bryts vid övergången mellan två medier.

Snell's lag kan härledas relativt enkelt på på flera olika sätt med hjälp av gymnasiematematik. Den intresserade eleven kan prova på detta i mån av tid! Jag har också gjort en härledning av Snell's lag här med hjälp av Fermats Princip.
| GeoGebra Appar | |
|---|---|
| Fy2-2.1 | Reflektion och brytning |
| Java Appar | |
|---|---|
| Fy2-2.2 | Reflektion och brytning |
Totalreflektion och fiberoptik (sid 63-64)
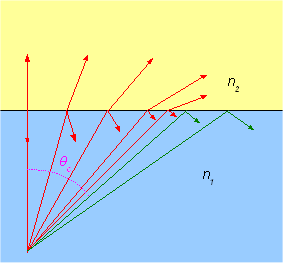
Ljus som går från ett "tjockare" till ett "tunnare" medium, som exempelvis från vatten till luft, kommer att brytas bort från normalen. Se bilderna nedan! Brytningsvinkeln blir då större än infallsvinkeln och det kommer att finnas en största infallsvinkel som man kallar gränsvinkeln $\alpha_g$. Gränsvinkeln bestäms av
$ n_1\sin \alpha_g=n_2 \sin 90^{\circ}$ $\Rightarrow$ $ \sin \alpha_g=\dfrac{n_2}{n_1}$

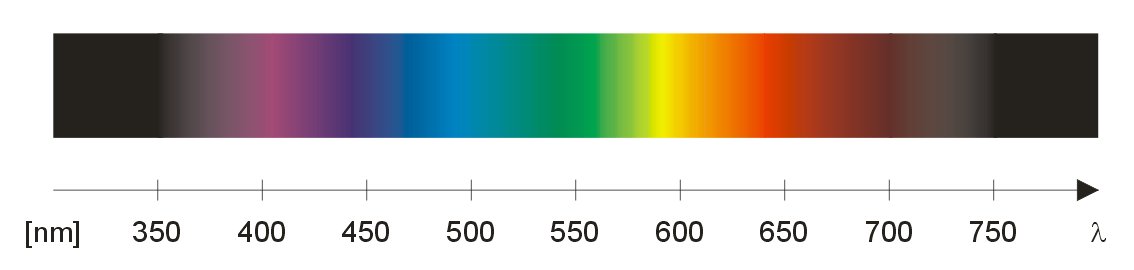
Spektrum av synligt ljus (sid 65-67)
Vanligt solljus består av alla färger, det visade Newton genom en rad kluriga experiment. Det syliga ljuset har våglängder från ungefär 400 nm (blått) till 700 nm (rött).
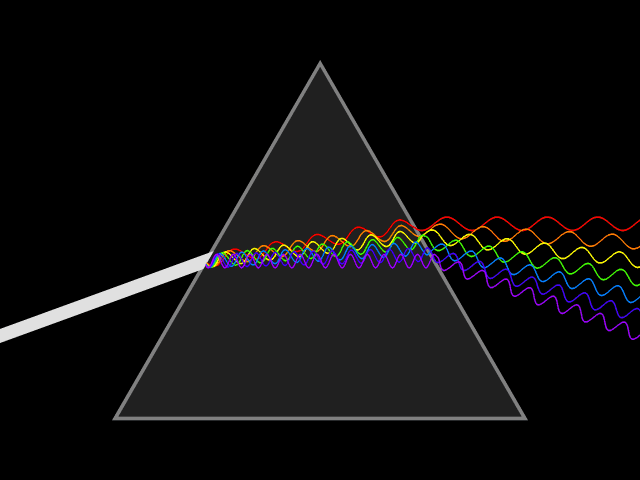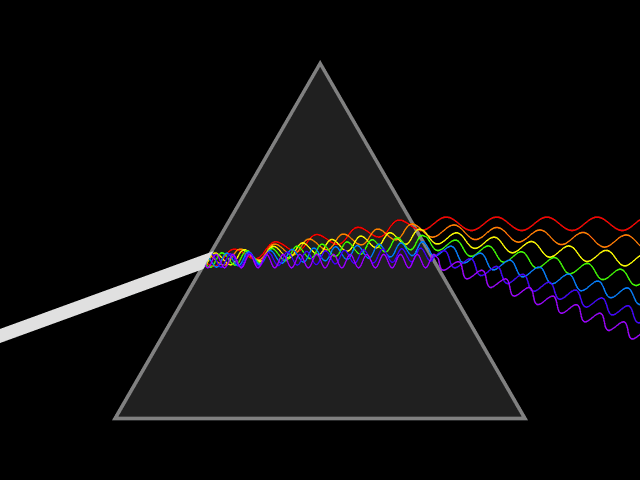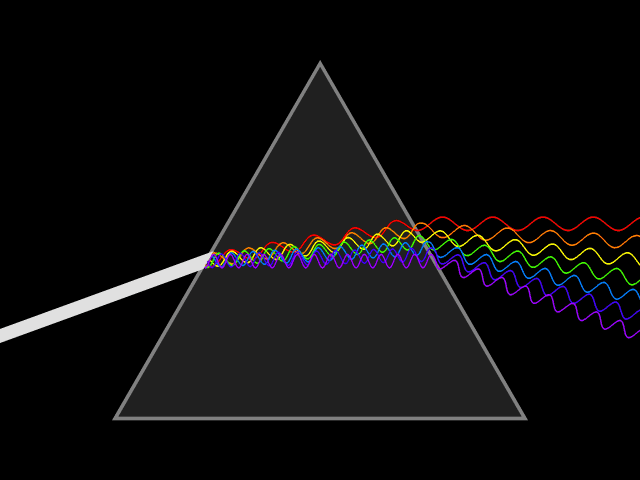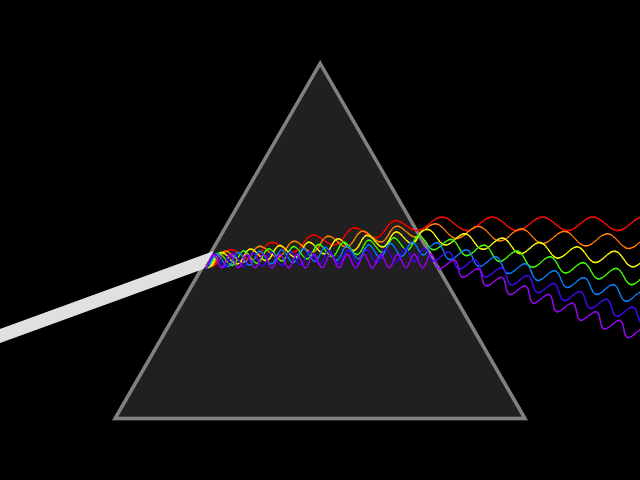
Så varför delas ljuset upp i olika färger när det bryts? Ja, eftersom olika färger bryts olika mycket så är det rimligt att anta att de olika våglängderna har olika brytningsindex! Och det är precis så det förhåller sig, denna egenskap hos ljus har ett eget namn, det kallas för ljusets dispersion eller färgspridning.
Lös 2.01,2.03-2.09,2.13,2.14
2.2 Böjning och interferens
Ljud till skillnad från ljus böjs i vår makroskopiska värld. Du kan höra ljud i ett rum utan att för den delen kunna se högtalarna som står i ett annat rum. Böjnings fenomenet kan lätt förväxlas med reflektion, exempelvis så är det naturligtvis så att en del av det ljud vi hör även delvis har reflekterats mot väggar och tak etc. När det gäller ljus, om någon tänder en lampa i ett angränsande rum och du kan märka detta, så beror detta enbart på reflektion och inte böjning. Förklaringen ligger i skalan på ljudets och ljusets våglängder. Att ljus kan böjas kan förklaras med vågmodellen och ett argument för att ljus verkligen kan ses som en vågrörelse.
Interferens med dubbelspalt (sid 69-72)
Thomas Young var den förste att observera att synligt ljus kunde bilda ett interferensmönster i sitt berömda dubbelspalts försörk. Han drog den korrekta slutsatsen att ljus har vågegenskaper.
När två vågor samverkar/interfererar skapas en enda våg och utslaget blir summan de två vågorna. Lek med GeoGebra appen för illustration av interferens av vågpaket.
Följande begrepp är viktiga:
Koherenta vågkällor = Vågkällor som svänger i takt med samma frekvens.
Monokromatiskt ljus = ljus med en bestämd våglängd, exempelvis laserljus.
Exempelvis vanligt solljus består av ljus av alla färger/våglängder och det är då varken monokromatiskt eller koherent.
LED-ljus är exempel på monokromatiskt ljus. Det består av endast en färg/våglängd (monokromatiskt), men vågorna är inte i fas, det är inte koherent.

Laser-ljus däremot är exempel på ljus av bara en färg/våglängd (monokromatiskt) och där även vågorna är i fas (koherent). Koherent ljus är alltså alltid även monokromatiskt, men omvändningen gäller ej!

Åter till dubbelspalts experimentet!
Kvantmekanikens kärna kan sammanfattas i Young's dubbelspalts experiment, det visar på att något fundamentalt annoulunda pågår i kvantvärlden jämfört med vad vi är vana vid från vår vanliga makroskopiska värld. Favoriten Jim Al-Khalili gör här ett mycket bra försök att förklara detta fenomen.
| Double Slit Experiment explained! by Jim Al-Khalili |
Den bok vi har, som är mycket bra överlag, är något otydlig i detta viktiga avsnitt! Jag skall försöka att förtydliga Young's Dubbelspalts experiment. För det första måste vi använda oss av en koherent ljuskälla, en laser ljuskälla med andra ord. Jag hittade en rätt bra animering över hur experiment fungerar, se nedan. Det koherenta ljuset kommer in från vänster böjs av i dubbelspalten och interfererar efter att det passerat spalten. Resultatet blir ett interferensmönster som ni ser längst till höger i animeringen, med mörka respektive ljusa partier om vartannat.
 |
Rory Coker |
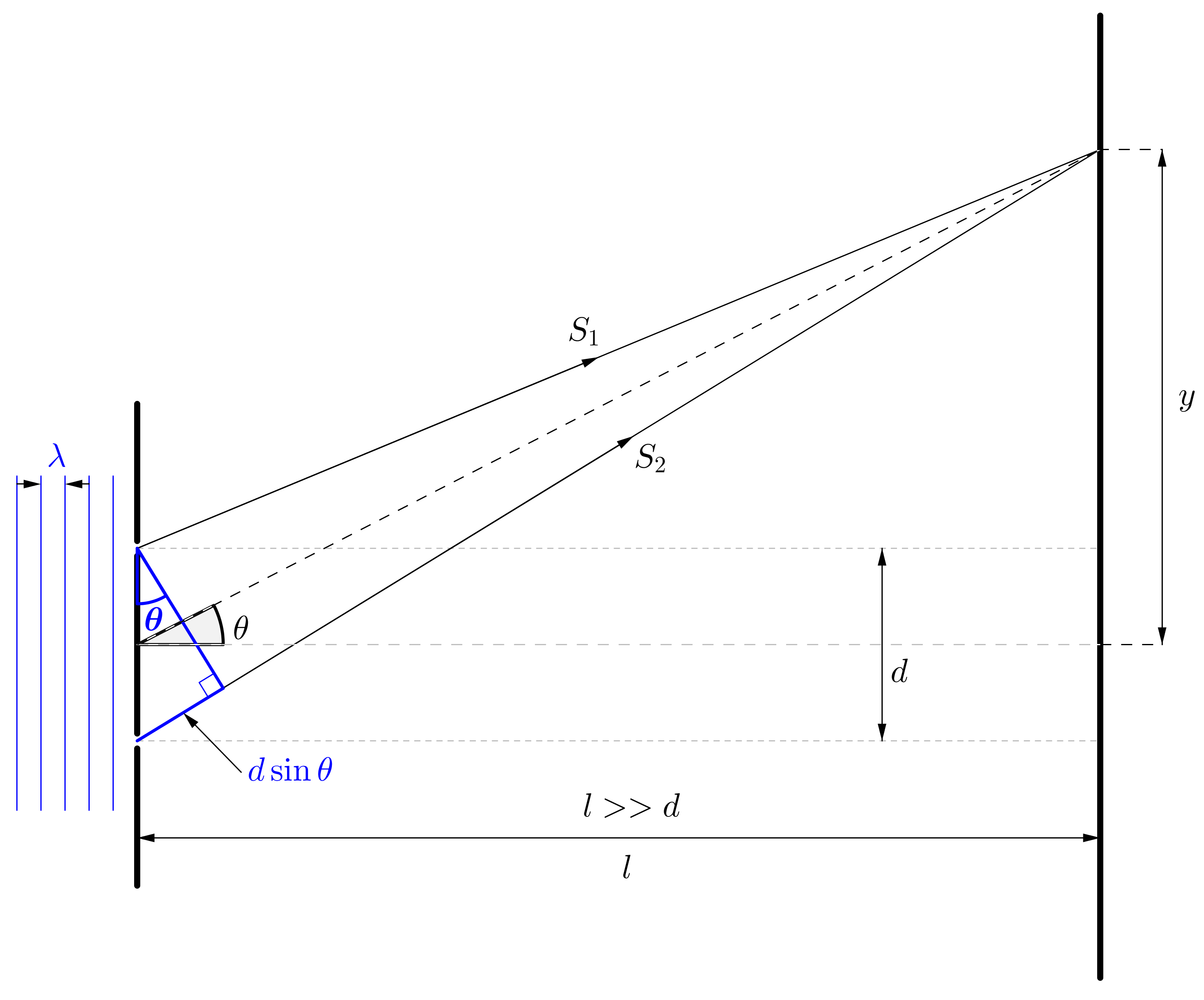
Nedan har jag gjort en principskiss för hur experimentuppställningen ser ut. Notera att avstånden inte på något sätt är proportionella! I verkligheten är $l>>d$ (läses "$l$ är mycket större än $d$"). Se figuren direkt under som lite bättre visar hur det egentligen ser ut, men även den är oproportionell.
Avståndet $l$ är i storleksordningen meter, medan avståndet $d$ är bråkdelar av mm!!! Det kan alltså skilja en faktor 10 000 eller 100 000 på dessa båda avstånd. Kontentan blir att strålarna $S_1$ och $S_2$ i stort sätt är parallella, vilket underlättar geometrin och matematiken.
Notera också att man i figuren även ser att $\tan \theta=\dfrac{y}{l}$. Där $y$ är avståndet mellan centralmaximum och n:te ordningens maximum eller minimum. Om vi antar att skärmen där interferensmönstret uppstår är avlägset i förhållande till avståndet mellan de olika maxima/minima, dvs. att $l>>y$, då har vi också att.
$\tan \theta \approx \sin \theta \approx \theta \approx \dfrac{y}{l}$.
Detta ger oss ett uttryck för avståndet $y$ mellan centralmaximum och de andra ordningarnas maxima/minima. Där $n$ är ordningstalet.
$ \sin \theta \approx \dfrac{y}{l}$ $\Leftrightarrow$ $d \sin \theta \approx \dfrac{dy}{l}$ $\Leftrightarrow$ $ n\lambda \approx \dfrac{dy}{l}$ $\Leftrightarrow$ $y\approx \dfrac{n\lambda l}{d}$.
Detta uttryck är mycket användbart rent praktiskt eftersom variablerna $y$, $n$ och $l$ alltid är lätta att bestämma. Vet man sedan spaltavståndet kan man direkt beräkna inkommande våglängd och tvärtom.
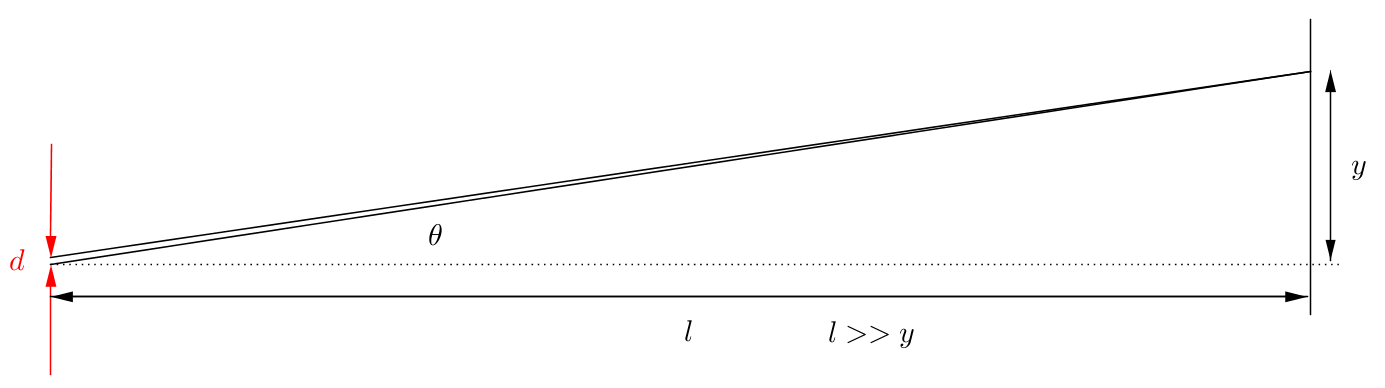
Något åt detta hållet ser det egentligen ut i verkligheten, men som sagt, även här blir avstånden missvisande!
Observera att $l$ även är mycket större än avståndet $y$ från centralmaximum till övriga maxima/minima!
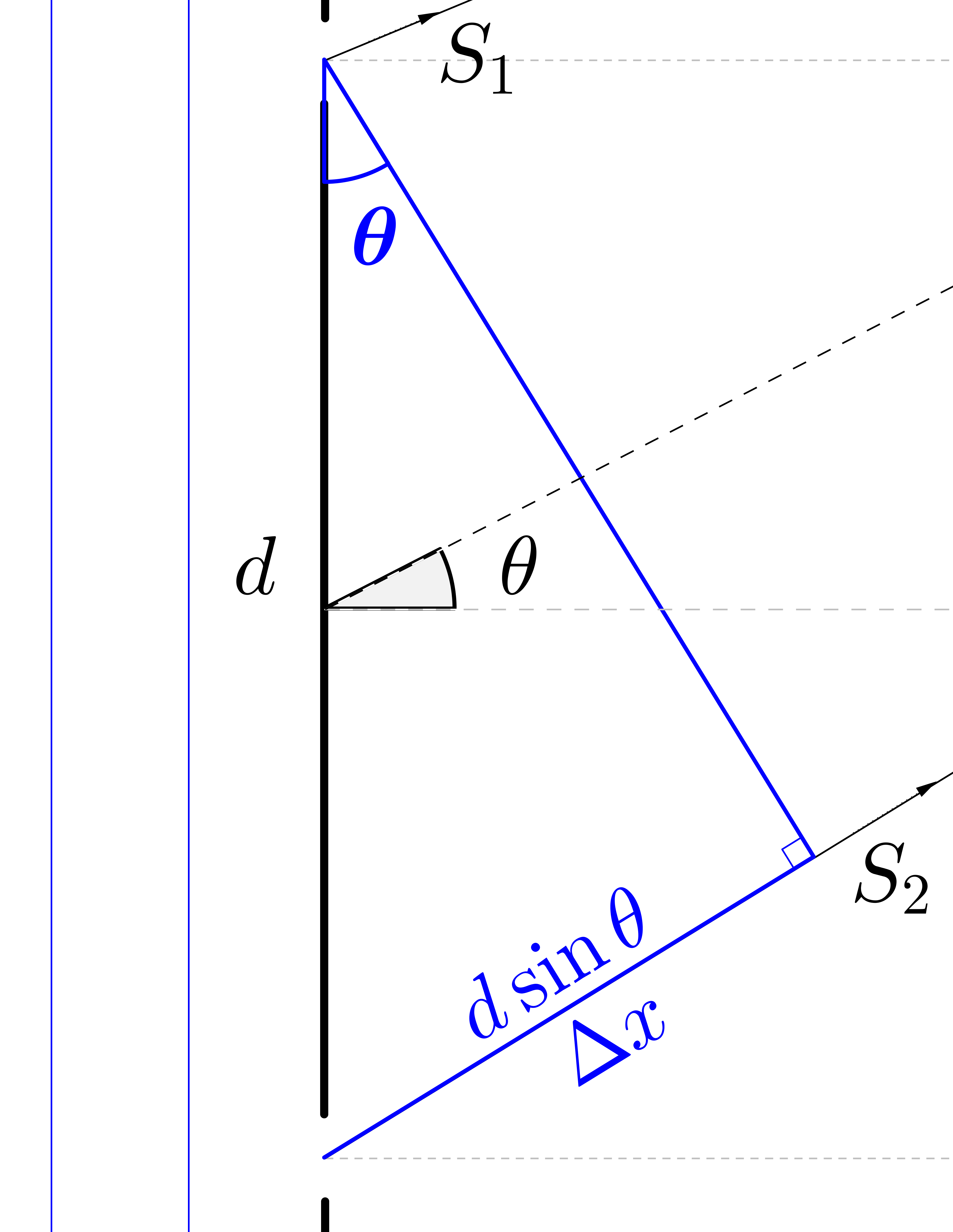
Här är den centrala geometrin uppförstorad! Man får att $\sin \theta = \dfrac{\Delta x }{d}$ $\Rightarrow$ $\Delta x=d\sin \theta$.
Så när skillnaden i längd mellan strålarna $S_1$ och $S_2$, här kallad $\Delta x$, är en multipel av den inkommande våglängden $\lambda$ får vi ett maximum och på motsvarande sätt när längdskillnaden är $\lambda/2$ erhålls ett minimum.
Vi kan sammanfatta detta med följande:
Konstruktiv interferens (Maximum): $d\sin \theta=n\lambda$, där $n\geq0$. Destruktiv interferens (Minimum): $d\sin \theta=n\lambda-\dfrac{\lambda}{2}= (n-\dfrac{1}{2})\lambda$ , där $n\geq1$. Centeravståndet:$y\approx \dfrac{n\lambda l}{d}$ |
Denna Java-app låter dig experimentera med dubbelspaltsförsöket, man kan justera våglängden på inkommande ljus $\lambda$, spaltöppningens storlek $d$ och avståndet till skärmen $l$.
Testa också denna lilla flash animering som på enkelt visuellt sätt illustrerar interferens.
Optiskt gitter (sid 72-75)
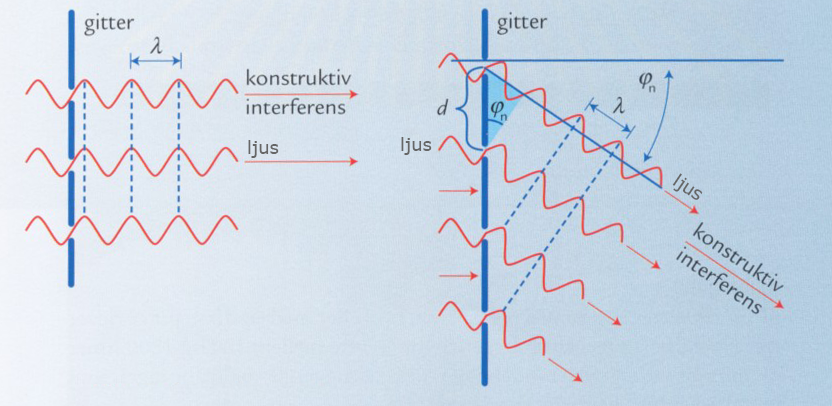
Ett optiskt gitter fungerar precis som dubbelspalten, men med många fler spalter, alla med samma inbördes avstånd $d$. Detta avstånd $d$ kallas för gitterkonstanten! Se figuren nedan.
Blandningsfärger (sid 76-78)
Varje spektralfärg, eller bara färg, har sin bestämda våglängd eller frekvens. Våglängd och frekvens hänger ihop enligt följande samband.
$c=\lambda\cdot f$, där $\lambda$ är våglängd, $c$ ljusets hastighet i vakuum och $f$ är frekvensen i Hz.
Varför är himlen blå på dagen och röd i solnedgången?
 Foto: Lars Fredriksson |
På väg ned mot jordens yta sprids ljuset med de kortaste våglängderna kraftigast. Det blå ljuset är den mest kortvågiga färgen i det synliga spektrum och därför sprids det väsentligt mer blått ljus över himlen än ljus i alla andra färger.
Himlen ser blå ut därför att blått ljus sprids ut lättast i atmosfären, Rayleigh-spridning. Ljuset från solen består av alla möjliga färger som blir vitt ljus tillsammans. När solljuset når jordens atmosfär blir de blå delarna av ljuset mer spridda åt olika håll, och vi ser blått överallt på himlen. Gult och rött har lättare att fortsätta rakt fram i samma riktning genom atmosfären. Det är också därför som solen ser rödare ut vid solnedgången. Då ser vi dess ljus från en så låg vinkel att det har passerat genom mer luft på sin väg mot oss. Det har passerat atmosfären "på snedden", vilket blir mycket längre sträcka genom atmosfären. Mer av det blåa ljuset har spritts bort, och endast det mest orange och röda ljuset går rakt igenom.
Ljuset från solen består av alla möjliga färger som blir vitt ljus tillsammans. Den blå färgen på himlen orsakas av att solljuset sprids mot luftmolekylerna i atmosfären. Det är de minsta molekylerna i atmosfären såsom syre (O2) och kväve (N2) som sprider ljusets färger olika. Större partiklar, till exempel vatten och damm, sprider ljus i stort sett oberoende av dess färg. Denna spridning, som kallas Rayleigh-spridning, har en mycket starkt våglängdsberoende som gynnar korta våglängder (den blå delen av det synliga spektrumet). Av denna anledning är det solljus som sprids ner till jorden i en stor vinkel med avseende på riktningen av solens ljus övervägande i den blå delen av spektrat. Se bilden nedan från wikipedia!
$I = {I_0}\dfrac{{8{\pi ^4}N{\alpha ^2}}}{{{\lambda ^4}{R^2}}}(1 + {\cos ^2}\theta )$
Ur denna intensistetsformel ser vi att
$I \sim \dfrac{1}{{{\lambda ^4}}}$
Rayleighspridningen är också orsaken till den röda solnedgången. Här är solstrålarnas väg genom atmosfären så lång att endast den mest "uthålliga" färgen finns kvar – nämligen rött. Det är också därför som solen ser rödare ut vid solnedgången. Då ser vi dess ljus från en så låg vinkel att det har passerat genom mer luft på sin väg mot oss. Det har passerat atmosfären "på snedden", vilket blir mycket längre sträcka genom atmosfären. Mer av det blåa ljuset har spritts bort, och endast det mest orange och röda ljuset går rakt igenom. 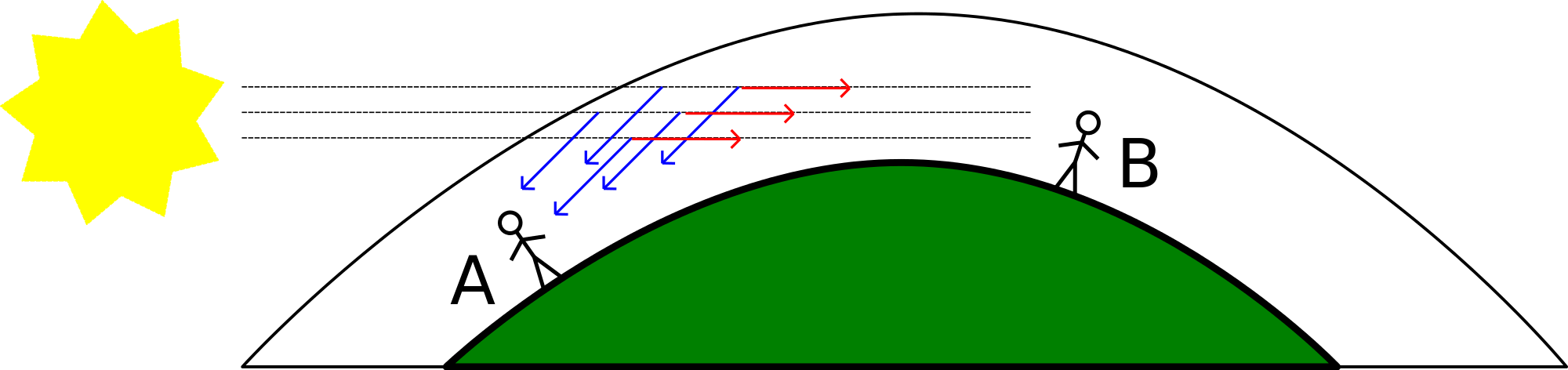
Lös 2.17-2.22, 2.24
2.3 Det elektromagnetiska spektret
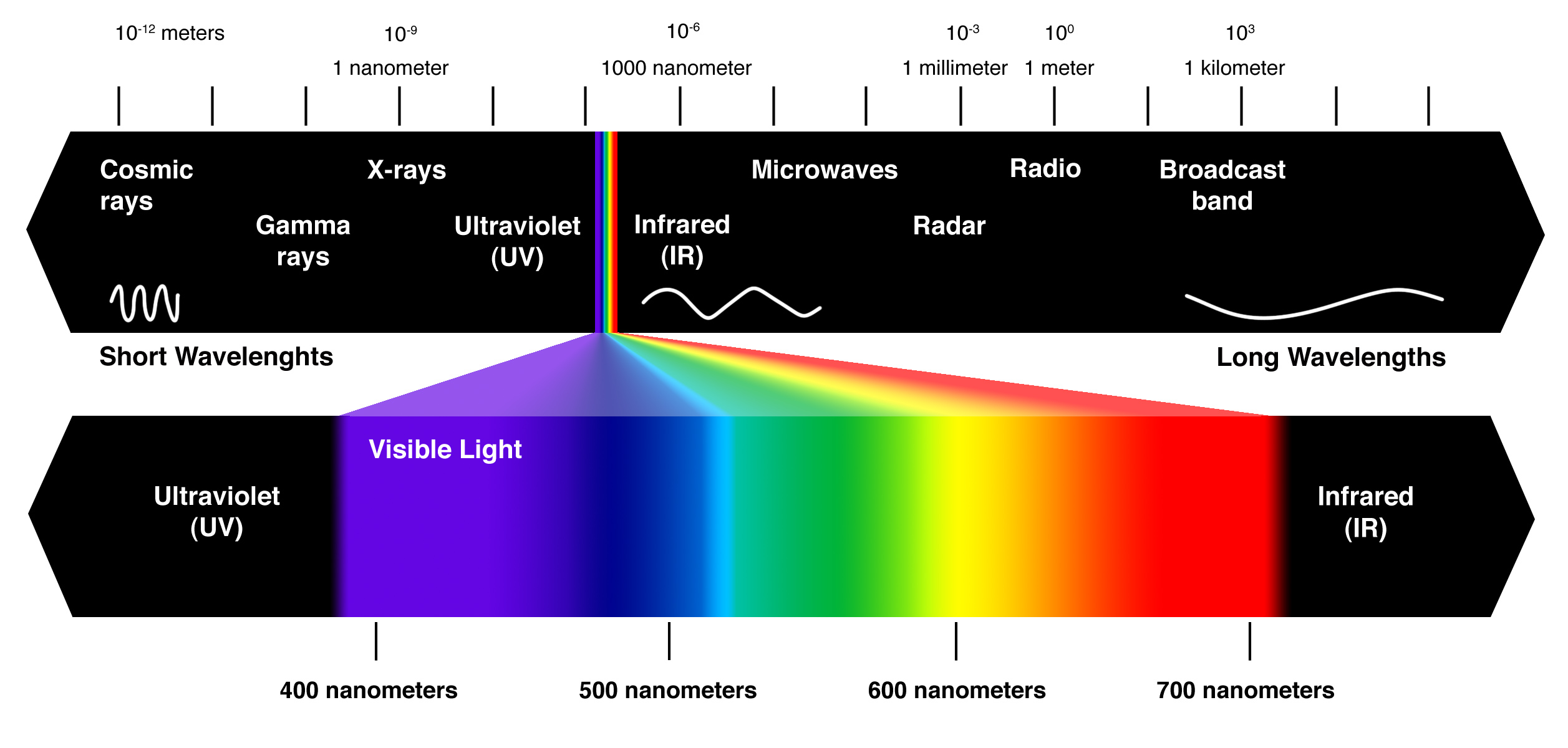
Radiovågor (sid 83-84)
Det är faktiskt bara i drygt 100 år som vi kunnat sända radiosignaler över långa avstånd runt vår planet. Fysiker trodde inte att detta skulle vara möjligt eftersom jorden är rund och vågorna breder ut sig rätlinjigt, men jonosfären reflekterade radiovågorna som en spegel. Det var Italienaren Guglielmo Marconi som utförde dessa framgångsrika experiment, Marconi var en utmärkt uppfinnare och insåg omedelbart radiovågornas potential. Han erhöll även senare Nobelpriset för denna uppfinning, vilket egentligen var rättså orättvist, framför allt mot Britten Oliver Lodge. Lodge var den fysiker som utarbetade den teoretiska grunden för trådlös telegrafi.