5.1 Gravitationsfält

Newtons Gravitationslag beskriver hur krafterna mellan kroppar (massor) kan bestämmas.

Newtons Gravitationslag	$F=G\dfrac{m_1m_2}{r^2} \textrm{, där } G=6.67\cdot 10^{-11} \textrm{Nm}^2 \textrm{/kg}^2$

Ett gravitationsfält är ett område där föremål påverkas av gravitationskrafter.

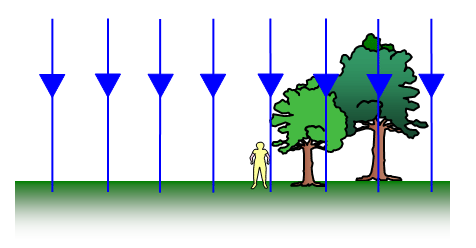
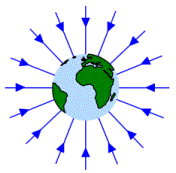
Gravitationsfältstyrka är ett mått på hur mycket ett föremål påverkas i ett gravitationsfält. Styrkan ges av.

Gravitationsfältstyrka	$g=\dfrac{F_g}{m} \textrm{, enheten för fältstyrka är N/kg}$

Kombineras dessa båda uttryck fås fältstyrkan vid ytan av en kropp, exempelvis Jorden. Det är detta vi kallar för tyngdacceleration, alltså gravitationsfältstyrka på ett visst ställe.

Tyngdacceleration	$g=\dfrac{GM}{r^2} \textrm{, om M är Jordens massa och r Jordens radie fås } g\approx 9.82$

Lös 5.01-5.05 och i mån av tid 5.06,5.07

 

5.2 Elektriska fält

Elektrisk fältstyrka är givet som kraft per laddning, mellan två metallplattor ges den elektriska fältstyrkan också som spänningen dividerat med avståndet mellan plattorna.

Homogent elektriskt fält, fältlinjerna ritas med jämna mellanrum!

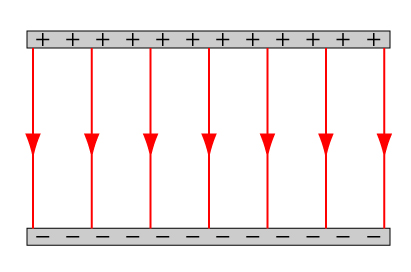
Elektrisk fältstyrka	$E=\dfrac{F}{q}=\dfrac{U}{s}$

Radiellt fält (sid 185-186)

Linjerna i figuren kallas elektriska fältlinjer och de visar riktningen på den elektriska fältstyrkan.

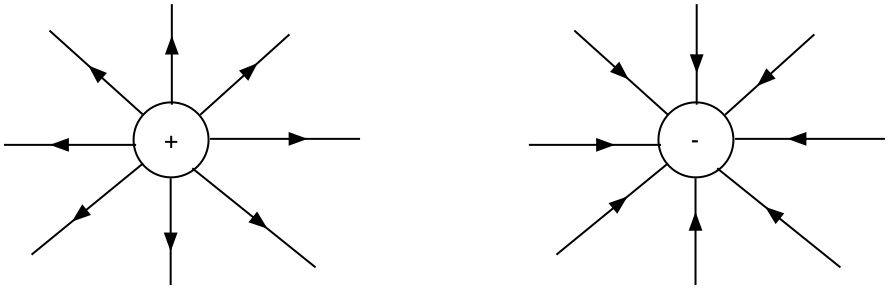
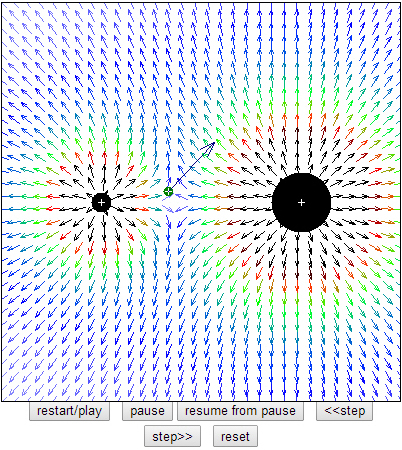
Om två olika laddningar påverkar varandra kommer fältlinjerna att anta nedanstående utseende. Notera också riktningen på testladdningarnas kraftvektorer!

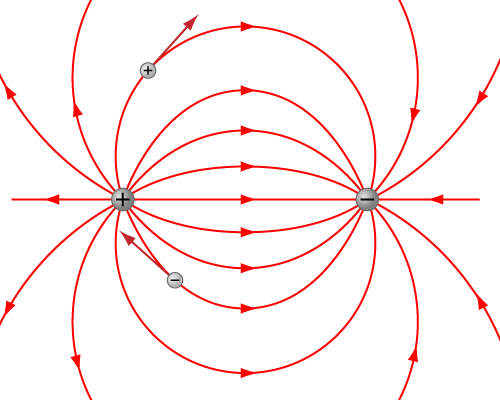
En provladdning påverkas av en elektrisk kraft $F$ som ges av Coulombs lag.

Coulombs lag	$F=k\dfrac{q_1q_2}{r^2} \textrm{, där } k=8.99\cdot 10^{9} \textrm{Nm}^2 \textrm{/C}^2$

Laborera med det Elektriska Fältet. Klicka på appleten här intill! Det finns ett antal olika konfigurationer att testa, exempelvis enkel positiv laddning eller olika stora olika laddningar! Testa er fram och se hur testladdningen beter sig! Ni kan också välja mellan att visa fältlinjer eller fältvektorer. Skärmbilden här intill visar fältvektorer och två olika stora positiva laddningar!

Kolla även denna Java-applet.

Lös 5.08-5.13,5.15

 

5.3 Potentiell energi

Påminner om potentiell

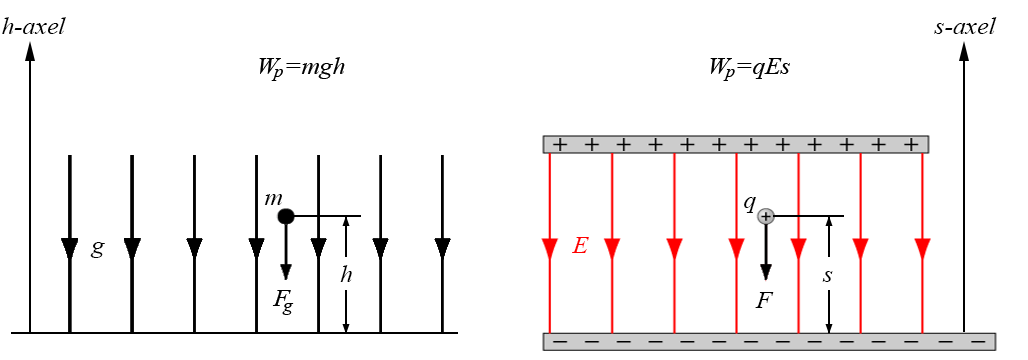
Homogent fält (sid 187-188)

Lös 5.18-5.20

5.4 Magnetiska fält

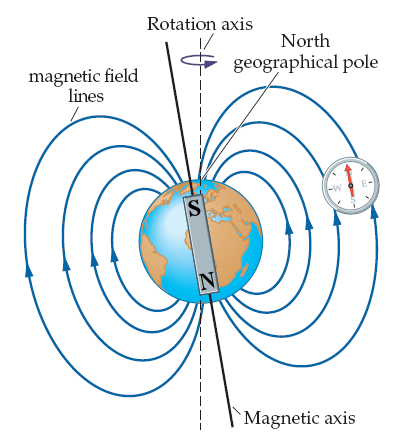
Jordens magnetfält är approximativt en magnetisk dipol med ena polen nära den geografiska nordpolen och den andra polen nära den geografiska sydpolen. En tänkt linje mellan de båda magnetiska polerna skulle luta med ungefär 11,3° mot jordensrotationsaxel.

Rent fysikaliskt är den magnetiska pol som finns nära nordpolen en magnetisk sydpol, eftersom en magnetisk nordpol dras mot den. Av samma anledning finns i fysikalisk mening jordens magnetiska nordpol vid sydpolen. I dagligt tal menar man dock magnetpolen vid nordpolen om man säger "magnetiska nordpolen" och tvärtom.

Lös 5.22-5.23

 

5.5 Strömledare i magnetfält

Magnetisk kraft på strömledare	$F=B\cdot I \cdot l$ $B$ är magnetisk fältstyrka, mäts i Tesla $T$. $I$ är strömmen genom ledaren, mäts i Amepere $A$. $l$ ledarens längd, mäts i meter $m$.

De tre storheterna $F, B, I$, alltså magnetisk kraft, magnetisk fältstyrka och ström genom ledaren är vektor storheter. Vilket innebär att de förutom sina belopp också har en riktning. Att räkna ut beloppet på den magnetiska kraften är bara att stoppa in i formeln ovan, vad som däremot kan vara lite klurigt är att avgöra vilken riktning denna kraft har. Dessa tre vektorer bildar ett så kallat högersystem och det innebär att vi kan ta hjälp av vår högerhand för att avgöra kraftens riktning (eller någon av de båda andra vektorerna beroende på vilken vi söker).

Man formulerar Högerhandsregeln!

Högerhandsregeln	Bilda ett ortogonalt koordinatsystem med hjälp av högerhandens tumme, pekfinger och långfinger! Tummen pekar i strömmens riktning $I$. Pekfingret pekar i magnetfältetsriktning $B$. Långfingret pekar i kraftens riktning $F$

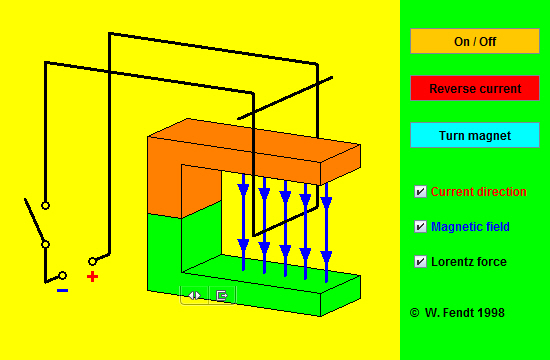
Testa och använd högerhandsregeln på flash animeringen nedan. En svävande ledare i form av ett aluminium folie som vi skickar ström igenom, ni kan styra strömriktningen! Se om ni får kraftriktningen att stämma!

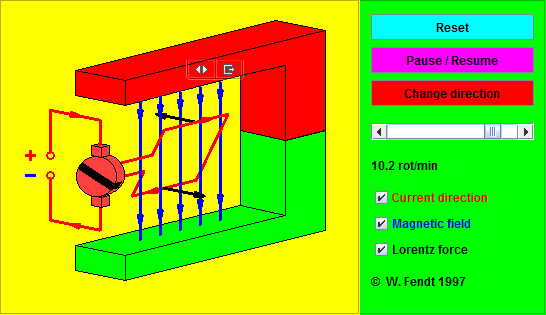
Nu går det att förklara de olika stegen i den elektriska motorn, försök att göra detta!

Lös 5.24-5.29

 

5.6 Magnetfält runt Strömledare

Raka ledare (sid 199-200)

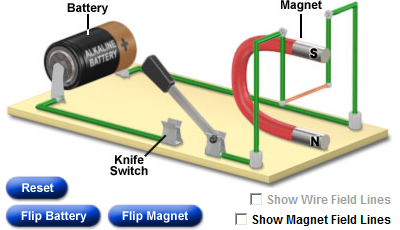
I ett experiment redan 1820 upptäckte Hans Christian Örsted (1777 - 1851) att kompasser påverkades när de närmade sig en ledning som genomfors av en elektrisk ström. När strömmen var avslagen, ställde kompassen som vanligt in sig mot norr – men när strömmen slogs till så slog nålen runt. Efter mer omfattande försök kunde han mer exakt slå fast hur och varför nålen rörde sig. En elektrisk ström ger nämligen upphov till ett magnetiskt fält runt omkring strömmen! Det bildades ett cirkulärt magnetfält med riktning enligt skruvregeln eller tumregeln. Två till synes helt separata fenomen: magnetism och elektricitet visade sig alltså höra samman. Detta anses allmänt vara 1800-talets kanske viktigaste upptäckt!

Kom ihåg!	Det finns ingen direkt motsvarighet till Coulombs lag för magnetisk kraftverkan! Denna kraft är annorlunda och mer komplicerad! Fram för allt, den magnetiska kraften är en konsekvens av laddningar i rörelse. Laddningar i rörelse alstrar ett magnetfält. Laddningar i rörelse påverkas av ett magnetfält.

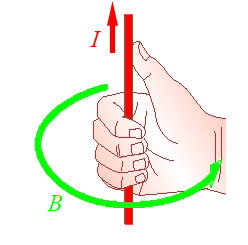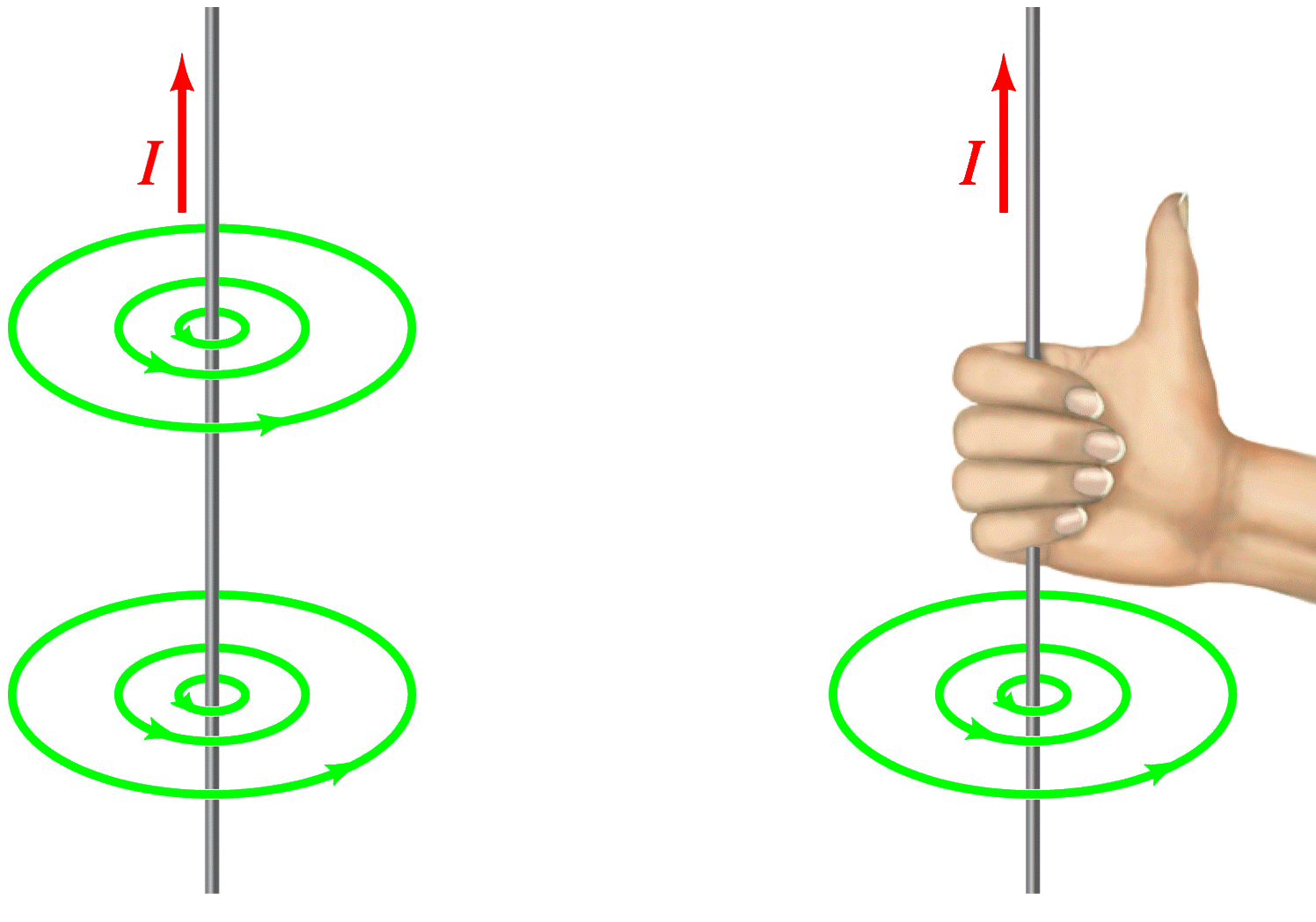Observera att de magnetiska fältlinjerna alltid bildar slutna kretsar. Vilket är en direkt konsekvens av att det ej finns magnetiska monopoler!

Biot­Savarts lag	Det magnetiska fältet är starkare nära ledaren och försvagas då avståndet till ledaren ökar. Fältet blir starkare då strömstyrkan ökar. Förhållandet mellan magnetisk flödestäthet, avstånd och strömstyrka beskrivs av Biot-Savarts lag: $B=\dfrac{\mu_0I}{2\pi r}$, där $\mu_0=4\pi \cdot 10^{-7}$ $\left[\dfrac{\rm{Tm}}{\rm{A}}\right]$ och kallas för permeabiliteten för vakuum.

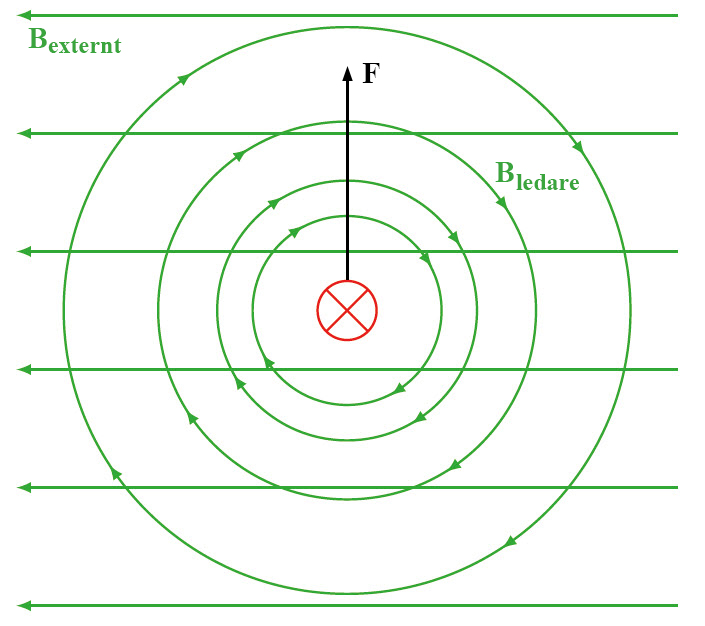
Kraften på en ledare i magnetfält Det bildas som sagt ett magnetfält kring en strömgenomfluten ledare, här kallad $B_{ledare}$. Om denna ledare i sin tur befinner sig i ett annat externt magnetfält, $B_{externt}$, kommer magnetfälten att adderas med riktning. I bilden här intill exempelvis kommer magnetfälet att förstärkas under ledaren och försvagas ovanför ledaren. Naturen strävar efter jämvikt och vill således ha jämnt och fint magnetfält överallt. Det innebär att naturen i det här fallet vill flytta ledaren uppåt för att jämna ut och det uppstår en kraft $F$ riktad uppåt på ledaren. Kraften beror av strömmen genom ledaren $I$ och hur lång ledaren är i magnetfältet $l$ samt magnetfältets storlek $B$. $F=B\cdot I \cdot l$ Magnetfältets riktning, strömriktningen och kraftens riktning ska vara vinkelräta enligt högerhandsregeln.

 

Kraften mellan två ledare

En ledare som det går ström genom skapar ett magnetfält kring ledaren.
Placerar man en annan ledare på avståndet r från den första ledaren som det går ström genom, kommer den nya ledaren att påverkas av magnetfältet från den första ledaren.

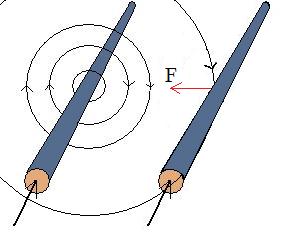
Kraften på en längd L av den högra ledaren blir
F = B I2 L
där I2 är strömmen i den högra ledaren och B kommer från den vänstra ledarens magnetfält.
B = μo · I1 /(2πr)
ger
F = μo · I1 /(2πr) · I2 · L

Om båda strömmarna går inåt kommer magnetfältet från den vänstra ledaren att vara riktat neråt där den högra ledare befinner sig. Högerhandsregeln ger då att kraften på den högra ledaren är riktad mot den vänstra ledaren.
Den högra ledaren skapar ett magnetfält där den vänstra ledaren befinner sig. Kraften på den vänstra ledaren blir då riktat mot höger.
Kraft och motkraft är lika stora och motsatt riktade.

Två parallella strömförande ledares 
magnetfält  påverkar elektronerna i 
ledarna så att det bildas en kraftverkan 
på dem. Därmed påverkas också 
ledarna som helhet.
Magnetfälten kring ledarna kan 
beskrivas med fältlinjer ­ då 
magnetfälten har motsatt riktning 
försvagas fältet, och då de har 
samma riktning förstärks fältet.

Amperes lag

Med hjälp av kraftverkan på ledarna 
definieras enheten för strömstyrka,
Ampere:
"En Ampere är den strömstyrka som 
ger upphov till en kraft på 2*10
­7
N/m 
på två strömförande ledare som är på 
en meters avstånd från varandra."
1.5.3 Amperes lag
Vi kan beräkna kraften på den ena 
ledaren med av Amperes lag:

$F_1=\dfrac{\mu_0I_2I_1l}{2\pi r}$

 

Magnetisk kraft mellan två ledare

Strömspolar (sid 200-201)

Om man lindar en elektrisk ledare runt t.ex. en toarulle så bildar ledningsvarven man lindat tillsammans en spiralliknande elektrisk komponent som kallas för en spole. En spole är intressant ur magnetisk synpunkt därför att varje varv i spolen bildar ett magnetfält i mitten av spolen när det går en ström i ledaren. Fältet är format som om det låg en stavmagnet inuti ledningsvarvet som bilden visar. Hur magneten ligger får du lätt fram med högerhandsregeln. ”Grabba tag” i ledningsslingan med högerhanden och lägg tummen i strömmens riktning så visar resten av fingrarna vilket håll fältet går genom och utanför slingan. I spolen sitter ju flera ledningsvarv bredvid varandra, och varje varv bidrar med ett likadant magnetfält. Varvens magnetfält bildar då tillsammans ett starkt magnetfält genom och runtom spolen.

 

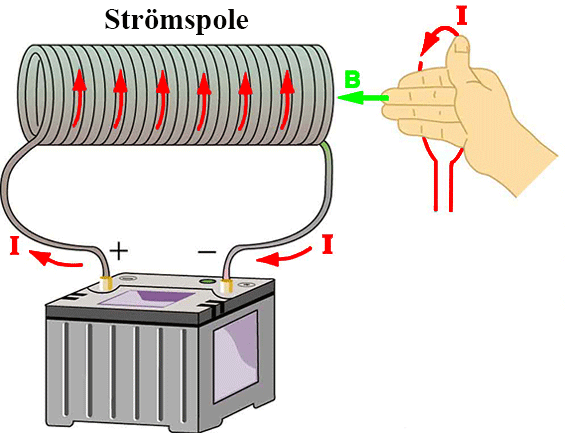
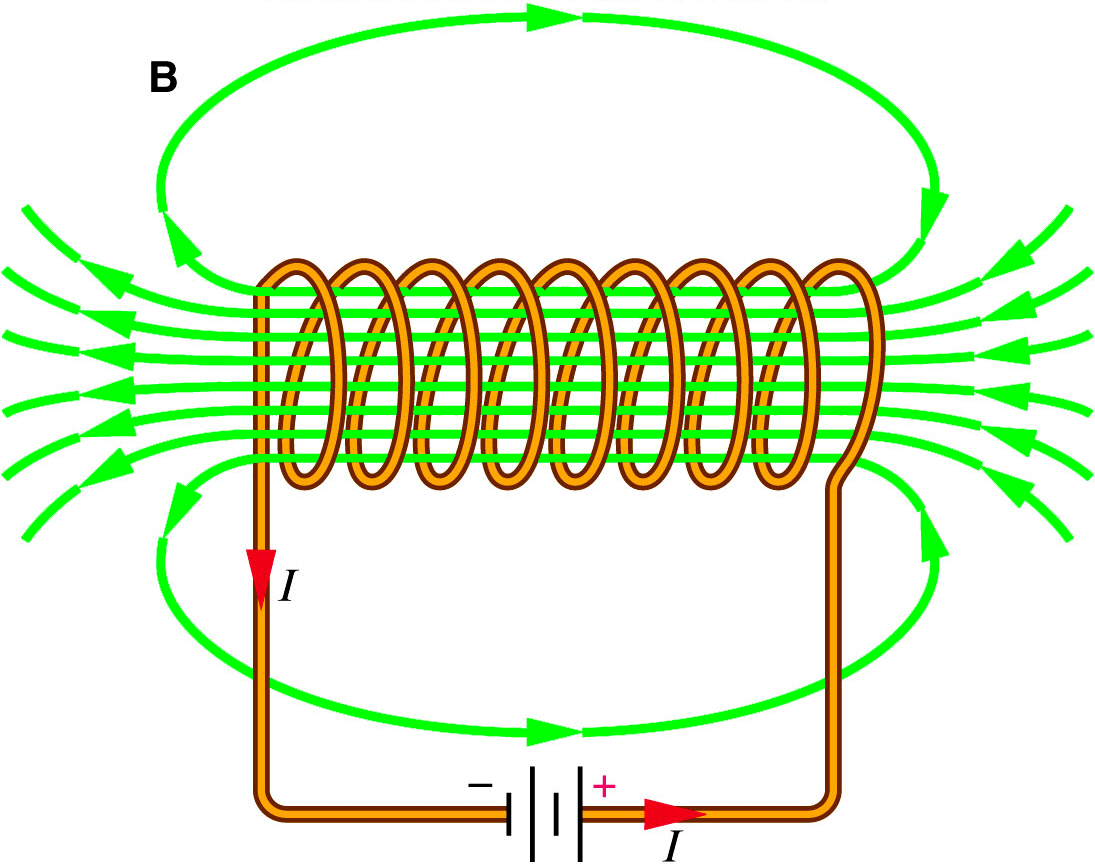
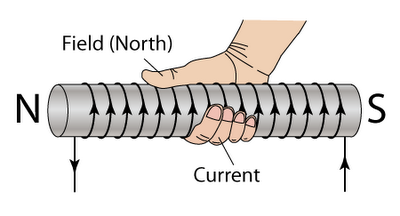
Elektromagneter

Om man sätter in en järnkärna i en strömsatt spole märker man att järnets magnetiska egenskaper och spolens magnetfält förstärker varandra, och man får en kraftig s.k. elektromagnet. Beroende på strömstyrka kan man reglera hur starkt elektromagnetens fält ska vara, och det går att tillverka mycket starkare elektromagneter än de ”naturliga” magneter som finns. Du har säkert sett magnetiska lyftkranar på bilskroten som lyfter flera tusen kilo, något som en vanlig magnet inte skulle klara. Fördelen med en elektromagnet är att magnetfältet upphör i samma ögonblick som strömmen bryts. Det är alltså avstängningsbara magneter vi pratar om!

Lös 5.32-5.35