2.1 Trigonometriska kurvor
Sinus- och cosinuskurvor (sid 52-55)
De trigonometriska funktionerna dyker upp i en rad olika sammanhang, inte enbart matematik, utan även inom fysik, kemi, teknik, medicin etc. Exempelvis svängande fjädrar, ljudvågor eller hjärtrytmen hos en människa.
Hur uppkommer då en sådan kurva, sinus eller cosinus? Lek med GeoGebra appen nedan så klarnar denna fråga.
| GeoGebra: | |
| Enhetscirkeln och sinusfunktionen | |
| Enhetscirkeln och cosinusfunktionen | |
| Enhetscirkel till trigonometrisk fkn. | |
| Sinus och cosinus | |
| Trigonometri med Enhetscirkeln | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Grafritande räknare (sid 56)
Öva gärna på att rita trigonometriska funktioner och söka lösningar till trigonometriska ekvationer på era respektive räknare! Jag har löst en uppgift, 2121 i boken. Här kan ni se hur ni skall ställa in era räknare och hur det går till på En Texas TI-84. Jag tycker personligen inte att detta är speciellt högprioriterat, det finns kraftfullare verktyg på nätet (WolframAlpha) och naturligtvis GeoGebra.
| GeoGebra: | |
| Enhetscirkel till trigonometrisk fkn. | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Förskjutna kurvor (sid 58)
Sinus- och cosinuskurvor kan manipuleras på 4 olika sätt,
$y=A \sin \left(k(x-B)\right)+ C$
genom att förändra dessa konstanter ( A, k, B & C) kan man sedan flytta, sträcka ut och trycka ihop "originalkurvan" på olika sätt. Testa detta i GeoGebra appen nedan.
| GeoGebra: | |
| Förskjutna kurvor | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Ekvationen för en sinusformad kurva (sid 60-61)
Detta har vi redan gått igenom ovan, kolla GeoGebra appen om ni är osäkra!
| GeoGebra: | |
| Förskjutna kurvor | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Kurvan $y=\tan x$ (sid 62-64)
Nu skall vi titta på den sista trigonometriska funktionen, tangensfunktionen.
Som man kan ana av namnet så anger tangens funktionen lutningen vid en viss given vinkel. Se återigen GeoGebra appen Enhetscirkel till trigonometrisk fkn.och skaffa er en känsla för hur detta hänger ihop. Notera också att periden för tangens är $180^{\circ}$ och att $\tan x$ inte är definierat för $x=90^{\circ}+n\cdot 180^{\circ}$. Detta beror på att $\cos x=0$ för dessa x-värden. När ni sedan löser ekvationer av typen $\tan x=k$ så man får två lösningar per varv. Dessa lösningar ligger mitt emot varandra i enhetscirkeln. Samtliga lösningar fås genom att man hittar en lösning (t.ex. med hjälp av räknedosa) och lägger $n\cdot 180^{\circ}$.
| GeoGebra: | |
| Enhetscirkeln och tangensfunktionen | |
| Tangensfunktionen | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Kurvan $y=a\sin x+b\cos x$ (sid 65-67)
Slutligen om man adderar en sinusfunktion och en consinusfunktion med samma period så får man en förskjuten sinuskurva. I boken är algebran för hur beskrivet denna omskrivning går till.Resultatet blir följande likhet.
$a \sin x + b \cos x = A \sin(x+v)$
Där $A = a^2+b^2$ och $ \tan v = \dfrac{b}{a} $ $\Rightarrow$ $v=\arctan \left(\dfrac{b}{a}\right)$
Det är en utmärkt övning att gå igenom algebran och försöka få en liten "aha" upplevelse...![]()
| GeoGebra: | |
| Superposition av Asin(ax) + Bcos(bx) | |
| Linjärkombination av sinus och cosinus | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Vill ni träna lite på att korrekt identifiera en förskjuten kurva så har jag hittat en Flashanimation som kallas Wave Rider.
2.2 Radianbegreppet
Ett nytt vinkelmått (sid 68-71)
På samma sätt som vi mäter exempelvis längd i olika enheter kan vi mäta vinklar i olika enheter, det är inget konstigt med det. I Sverige använder vi numera i princip alltid SI-enheter för längd, dvs. meter (m) och centimeter (cm) osv. I England/USA kör man fortfarande med yards (0.9144 meter) och inch (2.54 cm). Detta är egentligen inget problem, det är bara lite extra jobb att omvandla fram och tillbaka mellan enheterna. På samma sätt är det med de båda vinkelenheterna grader och radianer.
Definitionen av en radian är den vinkel som spänns upp i en cirkel då bågens längd är lika stor som radiens längd. Se animering nedan!

Att omvandla mellan grader och radianer är enkelt. Exempelvis ur animeringen ovan vet man att i varv i en cirkel har 360$^{\circ}$ eller $2\pi$ radianer.
Ett varv $=$ 360$^{\circ}=2\pi$ radianer. Man har alltså att
1$^{\circ}=\dfrac{\pi}{180} \approx 0.01745$ radianer.
1 radian $=\dfrac{180^{\circ}}{\pi} \approx 57.3^{\circ}$
OBS! Tänk på att ha era miniräknare korrekt inställda beroende på val av vinkelmått!
| GeoGebra: | |
| DEG to RAD and RAD to DEG Illustrator | |
| Radian Illustrator | |
| Circular functions | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Cirkelsektorn och radianer (sid 72-73)
Cirkelbågens längd står i direkt proportion till medlepunktvinkeln. Om medlepunktvinkeln $\theta$ i enhetscirkeln exempelvis är 47$^{\circ}$, då är längden $L$ av motsvarande cirkelbåge $2\pi \cdot \frac{47}{360}$ l.e (längd enheter).
Samma enkla resonemang gäller för arean av en cirkelsektor. Vi vet att arean av en cirkel är $A=\pi r^2$, så arean av en cirkelsektor blir då för samma medlepunktvinkeln som ovan $\pi r^2 \cdot \frac{47}{360}$ a.e (area enheter).
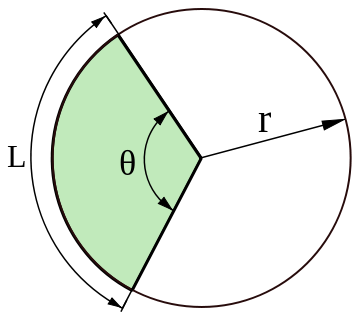
Om vinkeln $\theta$ istället mäts i radianer fås enligt samma resonemang:
$L=\dfrac{\theta}{2\pi} \cdot 2\pi r=\theta\cdot r$
$A=\dfrac{\theta}{2\pi} \cdot \pi r^2=\dfrac{\theta r^2}{2}=\dfrac{L\cdot r}{2}$
| GeoGebra: | |
| Arc Length and Sector Area | |
| Arc Length and Area of a Sector | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
2.3 De trigonometriska funktionernas derivator
Derivatan av $\sin x$ och $\cos x$ (sid 74-77)
Deriveringsreglerna för $\sin x$ och $\cos x$ är lätt att lära sig rent mekaniskt, men min förhoppning är att ni förvärvar en något djupare förståelse för varför det blir som det blir.
Att härleda derivatan till $\sin x$ och $\cos x$ kan göras på olika sätt beroende på vilka verktyg man har i sin matematiska verktygslåda! För gymnasie elever faller valet på derivatans definition, vilken ni bör vara bekanta med. Det räcker att härleda en av dessa, sedan kan man med hjälp av omskrivningar och kedjeregeln snabbt ta fram den andra.
Nyckeln till framgång ligger i att begripa följande så kallade standardgränsvärden.
\[ \lim_{h \to 0} \dfrac{\sin h}{h}=1 \quad \textrm{ och } \quad \lim_{h \to 0} \dfrac{\cos h -1}{h}=0\]
Att visa gränsvärdet för $\sin x/x$ tillhör den eftergymnasiala matematiken i exempelvis LTH-kursen endimensionell analys. Jonas Månsson har gjort en video där han härleder just detta gränsvärde. Den nyfikne studenten kan kolla här.
Nedan följer beviset för att $D_x \left({\sin x}\right) =\cos x$.
Om $f(x)=\sin x$ så ger derivatans definition att $\displaystyle f'(x)=\lim_{h \to 0} \dfrac { f (x + h)- f(x)} h$ .
$ \begin{aligned} D_x \left({\sin x}\right) & = \lim_{h \to 0} \frac { \sin \left({x + h}\right) - \sin \left({x}\right) } h &&\quad\text{Har satt in aktuell funktion} \\ & = \lim_{h \to 0} \frac { \sin \left({x}\right) \cos \left({h}\right) + \sin \left({h}\right) \cos \left({x}\right) - \sin \left({x}\right) } h &&\quad\text{Additionsformeln för $\sin(x+h)$} \\ & = \lim_{h \to 0} \frac { \sin \left({x}\right) \left({\cos \left({h}\right) - 1}\right) + \sin \left({h}\right) \cos \left({x}\right) } h &&\quad\text{Faktorisering av $\sin x$}\\ & = \lim_{h \to 0} \frac { \sin \left({x}\right) \left({\cos \left({h}\right) - 1}\right) } h + \lim_{h \to 0} \frac { \sin \left({h}\right) \cos \left({x}\right) } h &&\quad\text{Skriv som två gränsvärden}\\ & = \sin \left({x}\right) \ \lim_{h \to 0} \frac {\cos \left({h}\right) - 1} h + \cos \left({x}\right) \lim_{h \to 0} \frac {\sin \left({h}\right)} h &&\quad\text{Använd standardgränsvärdena} \\ & = \sin \left({x}\right) \cdot 0 + \cos \left({x}\right) \cdot 1 \\ & = \cos \left({x}\right) &&\quad\text{Klart!} \end{aligned} $
Att sedan visa att $D_x \left({\cos x}\right) =-\sin x$ följer direkt ur komplementlagarna för sinus och cosinus.
\[\boxed{\color{red}{\displaystyle \cos x= \sin \left({\dfrac \pi 2 - x}\right) }} \quad \textrm{och} \quad \boxed{\color{red}{\displaystyle \cos \left({\dfrac \pi 2 - x}\right)=\sin x }}\]
$ \begin{aligned} D_x \left({\cos x}\right) & =D_x \sin \left({\frac \pi 2 - x}\right) && \quad\text{Komplementlagen} \\ & =\cos \left({\frac \pi 2 - x}\right) \cdot (-1) && \quad\text{Kedjeregeln och andra komplementlagen} \\ &=- \sin x && \quad\text{Klart!} \end{aligned} $
OBS! Derivatan av dessa trigonometriska funktioner blir endast såhär eleganta om man använder vinkelmåttet radianer!
Om man nu istället låter $x$ representera grader och vill beskriva sinus utifrån detta så får man $f(x) = \sin(\dfrac{\pi x}{180})$. Derivera $f(x)$ och med hjälp av kedjeregeln erhålls $f'(x) = \dfrac{\pi}{180} \cdot \cos(\dfrac{x \pi}{180})$ - därmed har man även derivatan uttryckt från $\cos$ som tar radianer som argument. Byter vi ut $\cos$ mot $\cos_d$ - cos degrees alltså - får vi $f'(x) = \dfrac{\pi}{180} \cdot \cos_d(x)$.
Tänk så här: Om vi deriverar sinus med avseende på radianer så får vi sinus förändringshastighet per radianer. Deriverar vi istället sinus med avseende på grader får vi dess förändringshastighet per grader. Eftersom det finns 360 grader och $2\pi$ radianer på ett varv i en cirkel kommer förändringen av sinus per grad vara mindre än förändringen av sinus per radian. $1^{\circ}$ är ju $\dfrac{\pi}{180} \approx 0.01745$ gånger mindre än en radian, därmed är även förändringshastigheten hos sinus $\dfrac{\pi}{180} \approx 0.01745$ gånger mindre då vi ger sinus ett argument i grader istället för radianer.
En formell räkning skulle kunna se ut såhär.
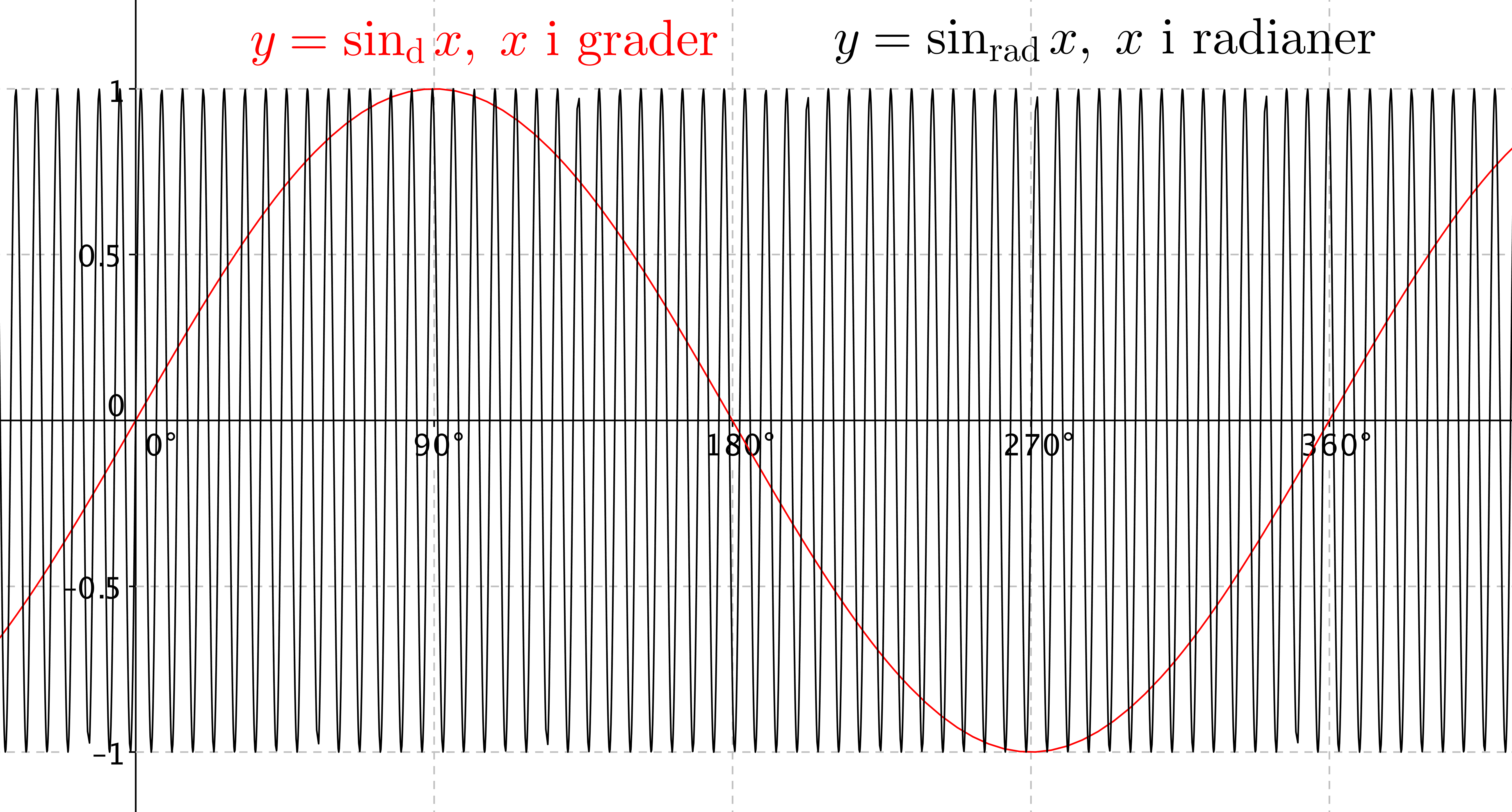
$\dfrac{d}{{dx}}{\sin_d }(x) = \dfrac{d}{{dx}}{\sin _{rad}}\left( {\dfrac{{\pi x}}{{180}}} \right) = \dfrac{\pi }{{180}}{\cos _{rad}}\left( {\dfrac{{\pi x}}{{180}}} \right) = \dfrac{\pi }{{180}}{\cos_d }\left( x \right) \approx 0.01745 \cos_d \left( x \right)$
Här har jag i samma graf ritat sinusfunktionen uttryckt i grader respektive radianer!
| GeoGebra: | |
| Derivatan av sinusfunktionen med radianer | |
| Derivatan av sinusfunktionen med grader | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Derivatan av sammansatta funktioner (sid 78-79)
Jag visar kedjeregeln för sammansatta funktioner.
$ \begin{aligned} y'(x) & = \mathop {\lim }\limits_{h \to 0} \frac{{y(x + h) - y(x)}}{h} &&\quad\text{Derivatans definition} \\ & = \mathop {\lim }\limits_{h \to 0} \frac{{f(g(x + h)) - f(g(x))}}{h} &&\quad\text{Förläng med $g(x+h)-g(x)$}\\ & = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(g(x + h)) - f(g(x))}}{h}} \right) \cdot \left( {\frac{{g(x + h) - g(x)}}{{g(x + h) - g(x)}}} \right) \\ & = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(g(x + h)) - f(g(x))}}{{g(x + h) - g(x)}}} \right) \cdot \left( {\frac{{g(x + h) - g(x)}}{h}} \right) &&\quad\text{Sätt $k=g(x+h)-g(x)$}\\ & = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(g(x) + k) - f(g(x))}}{k}} \right) \cdot \left( {\frac{{g(x + h) - g(x)}}{h}} \right) &&\quad\text{då blir $g(x+h)=g(x)+k$} \\ & = f'(g(x)) \cdot g'(x) &&\quad\text{Även $k \to 0$ Klart!} \end{aligned} $
| YouTube: | |
| Genomgång av kedjeregeln med exempel | |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||