2.1 Talteori
Delbarhet och primtal (sid 68-70)
Delbarhet hör direkt ihop med primtal. Primtalen är ju talens "atomer" skulle man kunna säga, de är byggstenarna.
Delbarhetsreglerna på sidan 69 kan hjälpa till en del vid räkneövningarna. Reglerna för delbarhet med 3 och 9 är inte helt uppebara att förstå, men när vi introducerat moduloräkning kommer det att bli lite tydligare.
Tänk på att om ni behöver ett udda tal i bevisföring så kan det alltid skrivas som $2k+1, \; \forall k\in \mathbb{Z}$ och på motsvarande sätt för ett jämnt tal $2k, \; \forall k\in \mathbb{Z}$.
Boken är också något kortfattad vad gäller begreppet delbarhet, den genomgångna övningen 2102 inför beteckningarna, men förklarar inte dem!
När man skriver $3|a$ så utläses detta som "3 är en delare i a" eller "3 delar a". Exempelvis $3|24$ därför att primfaktorn 3 finns med i faktoriseringen av talet 24.
$3|2\cdot 2 \cdot 2 \cdot3$
| Övningsuppgifter sidan 70 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2103 | 2104 | 2105 | 2106 | 2107 | 2108 | 2109 | 2110 | 2111 | 2112 |
| 2113 | 2114 | 2115 | 2116 | ||||||
Gemensamma och icke gemensamma faktorer (sid 71-73)
Begreppen i detta avsnitt har ni stött på tidigare utan att nämna dem vid namn! Minsta Gemensamma Multipel (MGM) exempelvis. Det är ju det ni gjort med nämnarna till ett antal bråk då ni bestämt minsta gemensamma nämnare.
$\dfrac{5}{18}+\dfrac{2}{21}$, minsta gemensamma nämnare fås enligt
$18= 2\cdot3\cdot3$
$21= 3\cdot7$
I MGM måste faktorer för att bilda båda dessa tal finnas med, alltså till 18 måste 2,3,3 finnas med och till 21 måste 3,7 finnas med. Vi får alltså:
$MGM(18,21)=2\cdot3\cdot3\cdot7=126$
och
$\dfrac{5}{18}+\dfrac{2}{21}=\dfrac{5\cdot 7}{2\cdot3\cdot3\cdot7}+\dfrac{2\cdot 2\cdot3}{2\cdot3\cdot3\cdot7}=\dfrac{35+12}{126}=\dfrac{47}{126}$
Största Gemensamma Faktor (SGF) eller Största Gemensamma Delare (SGD) som det också ibland skrivs handlar om att avgöra vilka primfaktorer talen har gemensamt. Här kommer också begreppet relativt prima in som fallet så två tal saknar gemensamma primfaktorer. Talen $a$ och $b$ säges vara relativt prima om $SGD(a,b)=1$.
| Synonyma benämningar för begrepp | |
|---|---|
| Största Gemensamma Faktor (SGF) | Minsta Gemensamma Multipel (MGM) |
| Största Gemensamma Delare (SGD) | |
| Greatest Common Factor (gcf) | Least Common Multiple (lcm) |
| Greatest Common Divisor (gcd) | |
Uppgiften 2125 är lite intressant, där introduceras ett rätt användbart samband, nämligen:
$SGF(a,b) \cdot MGM(a,b)= a\cdot b$
| Övningsuppgifter sidan 73 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2119 | 2120 | 2121 | 2122 | 2123 | 2124 | 2125 | 2126 | 2127 | 2128 |
| 2129 | 2130 | 2131 | 2132 | ||||||
Kongruens och moduloräkning (sid 75-78)
Ni är alla redan bekanta med moduloräkning sedan tidigare. Boken kallar detta för "klockaritmetik"och liknelsen är inte så dum i den meningen att man likställer tal som skiljer på en multipel av 12. Alltså när klockan pekar på 2:an är tiden inte entydigt bestämd! Den kan vara både 2 på natten och 2 på eftermiddagen (14). Man kallar talen 2 och 14 för kongruenta tal. Aritmetiken består bara av talen 0,1,…10,11, fast talen har inte entydig framställning.
Ett annat sätt att skriva detta är
$2\equiv 14 \pmod{12}$
vilket utläses "två är kongruent med fjorton modulo tolv". Jämför detta med bråk där också samma tal kan ha olika representanter. Det praktiska med moduloräkningen är att räknesätten +,−,⋅ beter sig "bra". Man kan byta representanter när som helst i sina räkningar. Antag t.ex. att vi vill beräkna $31\cdot 47 \quad (\textrm{mod}12)$. Ett alternativ är att räkna ut produkten och sedan byta representant
$31\cdot 47=1457=121\cdot 12 +5\equiv 5 \pmod{12}$
Man kan också byta till bättre representanter först och därefter utföra multiplikationen.
$31\cdot 47\equiv 7\cdot (-1) \equiv -7 \equiv 5 \pmod{12}$
Att dividera modulus är lite mer komplicerat och finns inte med i kursen.
| Övningsuppgifter sidan 77 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2136 | 2137 | 2138 | 2139 | 2140 | 2141 | 2142 | 2143 | 2144 | 2145 |
| 2146 | 2147 | 2148 | 2149 | 2150 | 2151 | 2152 | 2153 | 2154 | 2155 |
| 2156 | 2157 | ||||||||
Talsystem i olika baser (sid 80-81)
Vårt "vanliga" sätt att beteckna tal är ett positionssystem i basen 10. Det finns inget matematiskt skäl till att använda just denna bas, det är nog snarare en konsekvens av att vi har tio fingrar! Det finns inget som hindrar att man räknar i andra talbaser, exempelvis så är den binära (basen 2) och den hexagesimala (basen 16) dominerande bassystem i "datorsammanhang".
Från oktalt till decimalt:
$345_8=3\cdot 8^2+4\cdot 8^1 + 5\cdot 8^0=229_{10}$
Från decimalt till oktalt. Här får man göra en liten utredning, kolla först hur många siffror som behövs. I detta fallet krävs 3 siffror därför att $8^3=512$, vilket är större än vårt tal, alltså behöver vi inte en fjärde siffra! Kolla sedan resterna och "täck upp" med nästa position i det oktala systemet.
$229_{10}=3\cdot 8^2+4\cdot 8^1 + 5\cdot 8^0=345_8$
Babylonierna räkande i basen 60, vilket lever kvar i våra enheter för tid (60 sekunder på en minut, 60 minuter på en timme).
| Övningsuppgifter sidan 81 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2160 | 2161 | 2162 | 2163 | 2164 | 2165 | 2166 | 2167 | 2168 | 2169 |
| 2170 | 2171 | 2172 | 2173 | ||||||
RSA-kryptering (sid 82-83)
Det här är synnerligen intressant, av många anledningar. Jag tycker fram för allt att det är ett lysande exempel på när matematik i sin renaste form kommer till konkret praktisk nytta! Matematikens eller matematikernas konung Carl Friedrich Gauss kallade för övrigt talteorin för matematikens drottning. Läs gärna den här minibiografin och Gauss författad av Nationellt Centrum för Matematikutbildning (NCM).
Temat i boken är helt ok skrivet, men kortfattat! Torbjörn Tambour, docent i matematik vid Stockholms Universitet, utbildad och verksam under många år vid Lunds universitet har skrivit en bra artikel om RSA-kryptering, den är fullt möjlig att ta till sig för den ambitiöse gymnasisten.
Ännu bättre är Jonas Gustafsson & Isac Olofsson artikel RSA-kryptografi för gymnasiet. Detta är en gedigen och noggrann genomgång av konceptet från grunden. Texten täcker in hela kapitel 2 i boken och mycket mer därtill! Hela materialet kräver enbart gymnasiematematik!
Mer om kryptering och kombinatorik
Kryptering är ett område med mycket spännande kombinatorisk matematik. Ett annant exempel på kopplingen mellan matematik och kryptering eller i det här fallet attack mot kryptering är det så kallade födelsedags problemet (birthday problem or birthday paradox på engelska).
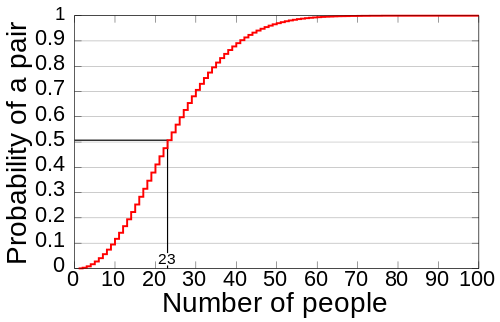
Födelsedags problemet eller födelsedagsparadoxen är ett rätt överraskande resultat på frågan om vad sannolikheten är att åtminstone två personer har samma födelsedag i en slumpmässigt utvald grupp!
Med hjälp av den så kallade lådeprincipen kan vi direkt dra slutsatsen att den aktuella sannolikheten är lika med 100 procent först då gruppen består av 366 personer! Beräkningarna är gjorda under förutsättning att året har 365 dagar och att varje dag på året (förutom 29 februari) är lika sannolika för en födelsedag.
Det överraskande resultatet är att för att sannolikheten skall bli 50% för att åtminstone två personer har samma födelsedag behövs endast en grupp om 23 slumpmässigt utvalda personer och om det i gruppen finns minst 57 personer, så är motsvarande sannolikhet större än 99 procent!
Matematiken bakom detta problem ledde till en välkänd kryptoattack som kallas födelsedag attacken, som använder denna sannolikhetsmodell för att minska komplexiteten i knäcka en hash-funktion.
Diagrammet nedan visar den beräknade sannolikheten för att åtminstone två personer skall dela födelsedag bland ett visst antal personer.
2.2 Talföljder
Inledning (sid 84-86)
| Talföljd: | En talföljd kan vara en ändlig eller en oändlig följd av tal uppställda efter en viss regel. I en talföljd kallas första talet för $a_1$, andra talet kallas för $a_2$, tredje för $a_3$ och så vidare. |
|---|
Talföljder kan presenteras genom att man helt enkelt skriver upp hela talföljden (om den är ändlig) eller delar av talföljden.
Exempel på talföljder:
$0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55\ldots$ , Fibonacci-talen
$5, 9, 13, 17, 21\ldots$
eller
$1, 3 ,6, 10, 15\ldots $
De tre punkterna $\ldots $ betyder att talföljden fortsätter enligt samma mönster.
Ett annat sätt att presentera en talföljd är att försöka hitta en formel eller ett uttryck för hur elementen i talföljden genereras. När man väl hittat mönstret och förstått hur talföljden genereras så är det sedan också ofta lätt att hitta den regel som genererar talföljden.
För att hitta mönstret i den mittersta talföljden ovan noterar man direkt att elementen är jämnt fördelade. Mellan två på varandra följande element skiljer det hela tiden 4! Man skulle kunna skriva talföljden enligt
$a_n=4n+1$
Detta sätt att skriva talföljden kallas för sluten form.
Ett annat alternativt sätt att skriva samma talföljd vore som
$a_n=a_{n-1}+4$
Detta sätt att beskriva hur elementen genereras kallas rekursiv form. Här genereras elementen med hjälp av sina föregångare.
Den slutna formen har fördelen att om jag vill veta element nummer 276, kan jag direkt få fram det genom
$a_{276}=4\cdot 276 +1=1105$
Det blir betydligt krångligare om man skulle använda sig av den rekursiva formen för att ta reda på $a_{276}$!
| Övningsuppgifter sidan 85 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2203 | 2204 | 2205 | 2206 | 2207 | 2208 | 2209 | 2210 | 2211 | 2212 |
| 2213 | 2214 | ||||||||
Rekursionsformler (sid 88-89)
Som sagt, den andra möjligheten att beskriva hur elementen genereras kallas den rekursiva formen. Talföljdens element uttrycks med hjälp av sina föregångare. Den tredje följden ovan, $1, 3, 6, 10, 15\ldots $, ni känner för övrigt igen den som triangeltalen. Här noterar man att skillnaden mellan två på varandra förljande tal hela tiden ökar med 1.
$a_2-a_1=3-1=2$
$a_3-a_2=6-3=3$
$a_4-a_3=10-6=4$
$a_5-a_4=15-10=5$
osv.
Det är således rimligt att anta att nästa element är 6 större än det sista vi vet. Alltså $15+6=21$. Så hur skall vi nu hitta regeln eller det matematiska uttryck som genererar talföljden? Man vill alltså hitta ett uttryck för det n:te elementet $a_n$. Element för element ser man att
$a_2=a_1+2$
$a_3=a_2+3$
$a_4=a_3+4$
$a_5=a_4+5$
osv
Detta kan vi sammanfatta som det rekursiva uttrycket
$a_n=a_{n-1}+n$
Vilket även stämmer för det första elementet, om man antar att $a_0=0$ blir $a_1=a_0+1=1$. Nästa element i talföljden blir alltså $a_6=a_5+6=15+6=21$.
Skall vi skriva rekursionformeln helt korrekt i detta fall måste vi ange var rekursionen skall starta.
$a_n=a_{n-1}+n$, med $a_0=0$ och $a_1=1$
Talföljder och rekursionsformler är ett gigantiskt område av matematiken och också ett område som överlappar många andra grenar av matematiken. Som vi såg ovan med talföljden $5, 9, 13, 17, 21\ldots$ kunde vi hitta en representation av denna på både sluten och rekursiv form. Ett mycket intressant fråga, som tyvärr ligger utanför gymnasiematematiken handlar om hur man kan översätta mellan rekursionsformler och slutna formler och också när detta är möjligt.
| Övningsuppgifter sidan 89 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2216 | 2217 | 2218 | 2219 | 2220 | 2221 | 2222 | 2223 | 2224 | 2225 |
| 2226 | 2227 | ||||||||
Aritmetiska talföljder (sid 90-91)
| Aritmetisk Talföljd: | En aritmetisk talföljd genereras genom att man till ett godtyckligt startvärde successivt adderar en konstant. |
|---|
Ett exempel på en sådan talföljd är talföljden ovan, där man successivt adderade konstanten 4.
$5, 9, 13, 17, 21\ldots$
Om vi fortsätter denna talföljd upp till ett visst element $n$ inser man snabbt att summan av en aritmetisk talföljd ges av
$S=\dfrac{\textrm{''första termen"} + \textrm{''sista termen''}}{2} \cdot \textbf{''antalet termer''} = \dfrac{a_1+a_n}{2} \cdot n$
Om man vill ta reda på hur många termer en talföljd har får man vara lite försiktig och tänka efter en aning. Jämför följande exempel. Vi tar vår talföljd igen och vill veta hur många termer summan har.
$5, 9, 13, 17, 21\ldots,497,501$
"Största termen" minus "minsta termen", alltså $a_n$-$a_1$ dividerat med term mellanrummet, 4 i detta fall. Detta ger ju antalet mellanrum, men vi ville veta antalet termer och det är 1 större!
$\dfrac{501-5}{4}=124$ och $124 +1 = 124$
Så 125 termer! Detta kan vi också få fram direkt om vi har den slutna formen, vilket vi har i detta fall.
$a_n=4n+1$ $\Longrightarrow$ $n=\dfrac{501-1}{4}=125$
| Övningsuppgifter sidan 91 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2229 | 2230 | 2231 | 2232 | 2233 | 2234 | 2235 | 2236 | ||
Geometriska talföljder (sid 92-94)
En geometrisk talföljd genereras genom att man till ett godtyckligt startvärde successivt multiplicerar en konstant. Ett exempel på en sådan talföljd är
$2, 6,18,54, 162, 486 \ldots$
som startar med $a_1=2$ och sedan multiplicerar man successivt med $k=3$3. Nu indikerade jag att talföljden pågår i all oändlighet i och med de tre avslutande punkterna $\ldots$. Men låt säga att jag vill beräkna summan av ett ändligt antal av denna talföljds element, exempelvis
$S=2+6+18+54+ 162+486$
Detta låter sig göras genom följande lilla trix.
Skapa summan $3S$
$\begin{aligned}
3S&=3\cdot 2+3\cdot 6+3\cdot 18+3\cdot 54+ 3\cdot 162+3\cdot 486 =\\
& =6+18+54+162+486+1458
\end{aligned}
$
Summan $3S$ är bara en annan del av samma talföljd som summan $S$ och vi kan skriva
$3S-S=S(3-1)=1458-2$
och man får summan $S$ som
$S=\dfrac{1458-2}{3-1}$
Försök själva visa det generella fallet för summan $S$ då första talet kallas $a_1$, faktorn kallas $k$ och man har $n$ element. Man får
$S=\dfrac{a_1 \cdot(k^n-1)}{k-1} = \dfrac{a_1 \cdot(1-k^n)}{1-k}$
| Övningsuppgifter sidan 94 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2240 | 2241 | 2242 | 2243 | 2244 | 2245 | 2246 | 2247 | 2248 | 2249 |
| 2250 | 2251 | 2252 | 2253 | 2254 | |||||
Ekonomiska, natur- och samhällsvetenskapliga tillämpningar (sid 96-100)
Flex exempel på övningar med talföljder.
| Övningsuppgifter sidan 98 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2257 | 2258 | 2259 | 2260 | 2261 | 2262 | 2263 | 2264 | ||
| Övningsuppgifter sidan 100 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2267 | 2268 | 2269 | 2270 | 2271 | 2272 | 2273 | |||
2.3 Induktionsbevis
Induktionsbevis är en viktig och kraftfull "bevisteknik" som man kan/måste använda om man vill visa att ett påstående är sant för alla positiva heltal. Ofta handlar det om en likhet men i princip kan det vara fråga om vilket påstående som helst. Att verifiera påståendet för ett heltal i taget är ju omöjligt eftersom det finns oändligt många heltal. Notera också att induktionsprincipen i sig är en mycket viktig egenskap hos de naturliga talen. Heltalen har helt enkelt definierats med egenskapen (de så kallade axiomen för de hela talen) att induktionsprincipen ska fungera.
Huvuddragen för Induktionsprincipen bygger på tre steg:
1 - Basfallet: Visa att påståendet är sant för ett första tal, vanligen 0 eller 1. Säg $n=1$.
2 - Induktionsantagandet: Antag att påståendet ät sant för ett fixerat men godtyckligt heltal $n=p$.
3 - Induktionssteget: Visa nu att under förutsättningen från 2 så är påståendet korrekt för $n=p+1$, dvs för nästa heltal.
Induktionprincipen ger nu att påståendet måste vara sant för alla heltal! Vi vet nämligen att det är sant för $n=1$. Och eftersom det är sant för $n=1$ så måste det enligt punkt 2 och 3 vara sant för $n=2$. Eftersom det nu är sant för $n=2$ måste det vara sant för $n=3$ etc.
Exempel:
Visa att om $n$ är ett positivt heltal så är summan
$S_n=1+2+3+4+5+ \ldots +n=\dfrac{n(n+1)}{2}$
Bevis:
1 - Basfallet: Visa först att påståendet/satsen stämmer då $n=1$.
Om $n=1$ så är å ena sidan $1+2+3+...+ n = 1$. Å andra sidan är $\dfrac{n(n+1)}{2}=\dfrac{1(1+1)}{2}=\dfrac{2}{2}=1$.
Satsen verkar stämma då $n = 1$.
2 - Induktionsantagandet: Anta nu att satsen stämmer för det positiva heltalet $n=p$. Det är detta steg i beviset som kallas induktionsantagandet. Det gäller sedan att visa att satsen då även stämmer för nästa heltal, $n=p+1$.
3 - Tillämpa induktionsantagandet: Alltså visa att
$1+2+3+4+5+ \ldots + p + (p+1)=\dfrac{(p+1)(p+2)}{2}$
Nu gäller det att med lite smart algebra och induktionsantagandet visa likheten. Gruppera exempelvis såhär
$\begin{aligned}
1+2+3+4+5+ \ldots +p +(p+1)&=(1+2+3+4+5+ \ldots +p) +(p+1) \\
&
= \dfrac{p(p+1)}{2} + (p+1) \quad \textrm{(Induktionsantagandet)}\\
&=
(p+1)\left(1+\dfrac{p}{2}\right) \quad \textrm{(Faktorisera!}\\
&
=\dfrac{(p+1)(p+2)}{2}
\end{aligned}
$
Så nu kan vi sammanfatta: Satsen stämmer för det positiva heltalet $n=1$. Om nu satsen stämmer för det positiva heltalet $n=p$ och man kan visa att satsen då också stämmer för nästa positiva heltal, $(n=p+1)$. Då har man enligt principen för matematisk induktion visat att satsen stämmer för alla positiva heltal.
| Övningsuppgifter sidan 107 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2304 | 2305 | 2306 | 2307 | 2308 | 2309 | 2310 | 2311 | 2312 | 2313 |
| 2314 | 2316 | 2317 | |||||||
Diagnos 2 och Blandade övningar kapitel 2
| Diagnos 2 sidan 111 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | |||||||
| Blandade övningar Kapitel 2 UTAN räknare sidan 112 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | |||||||||
| Blandade övningar Kapitel 2 MED räknare sidan 113 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 |
Blandade övningar kapitel 1-2
| Blandade övningar Kapitel 1-2 UTAN räknare sidan 114 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | ||||||||
| Blandade övningar Kapitel 1-2 MED räknare sidan 115 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 |
| 33 | |||||||||