Extrauppgifter i Fysik 2!
Här finns relevanta uppgifter från gamla frisläppta provbanksprov, men även en hel del andra bra övningsuppgifter från diverse olika källor. Gemensamt är att de alla motsvarar kursen Fysik 1 och den komman GY25 kursen Fysik nivå 1b.
Du kan filtrera uppgifter efter Avsnitt, Moment, Taggar och Nivå. Använd filtreringsalternativen ovan och klicka på "Filtrera" för att visa relevanta uppgifter.
Lycka till med Fysiken!
Om din skärm har låg upplösning går det bra att zooma i din webbläsare för att bättre se uppgifterna och lösningarna. Jag har valt att ha menyerna synliga överst hela tiden, bland annat för att snabbt kunna filtrera om, men även för att kunna ta sig till andra sidor smidigt.
| g-001 | Skriv $36{,}7\cdot 10^6$ g med SI-enheten för massa på grundpotensform. $\textbf{(1/0/0)}$ | |||||||||
|
||||||||||
SI-enheten för massa är kilogram och kilo (k) på 10-potensform blir $10^3$. k $\equiv 10^3$, (uttalas, prefixet k är ekvivalent med 10-potensen $10^3$). Vi får då räkningen. $\begin{align*}
36{,}7\cdot 10^6\textrm{ g}&=36{,}7\cdot 10^3 \cdot 10^3\textrm{ g}=36{,}7\cdot 10^3\textrm{ kg} =3{,}67\cdot 10^4 \textrm{ kg} &&
\end{align*}$
|
||||||||||
| g-002 | Ett klot av bly har volymen 1,4 dm$^3$. Bestäm klotets massa. $\textbf{(1/0/0)}$ | |||||||||
|
||||||||||
Densiteten för bly är 11,3 g/cm$^3$, det hittar man på sidan 7 i formelsamlingen. Volymen 1,4 dm$^3=1\,400$ cm$^3$. Massan för klotet ges ur $\begin{align*}
\varrho&=\dfrac{m}{V} \quad \Longrightarrow \quad m=\varrho \cdot V= 11{,}3 \cdot 1\,400 =15{,}82 \textrm{ kg} &&
\end{align*}$
|
||||||||||
| g-003 | Skriv 810 nm utan prefix med lämplig potens. $\textbf{(1/0/0)}$ | ||||||||
|
|||||||||
Prefixet n (nano) är ekvivalent med 10-potensen $10^{-9}$. $\begin{align*}
810\textrm{ nm}&= 810\cdot 10^{-9} \textrm{ m} &&
\end{align*}$
detta duger gott, men man skulle kunna skriva på grundpotensform också $\begin{align*}
&=\left(8{,}10 \cdot 10^2\right) \cdot 10^{-9}\textrm{ m}=8{,}10 \cdot 10^{-7}\textrm{ m}
\end{align*}$
|
|||||||||
| g-004 | Vilken sträcka är längst a) eller b)?
|
||||||||
|
|||||||||
|
|||||||||
| g-005 | Längdomvandlingar.
|
||||||||
|
|||||||||
|
|||||||||
| g-006 | Areaomvandlingar.
|
||||||||
|
|||||||||
|
|||||||||
| r-001 | En curlingsten skjuts iväg och stannar efter 14 s då den glidit 25 m. $\textbf{(1/1/0)}$ Vilken var stenens utgångshastighet? |
||||||||
|
|||||||||
Deaccelerationen fås ur definitionen, dvs. $\begin{align*}
a&=\dfrac{\Delta v}{\Delta t}=-\dfrac{v_0}{14}&&
\end{align*}$
Använder vi sedan sträckformel 2 kan $v_0$ bestämmas. $\begin{align*}
s&=v_0t+\dfrac{at^2}{2} \quad \Longrightarrow \quad 25=v_0\cdot 14 - \dfrac{\dfrac{v_0}{14}\cdot 14^2}{2} \quad \Longrightarrow \quad v_0=\dfrac{25}{7}\approx 3.6\textrm{ m/s}&&
\end{align*}$
Prova också att rita en vt-graf, det blir nästan ännu tydligare. Arean av den triangel som representerar rörelsen ger då svaret direkt! 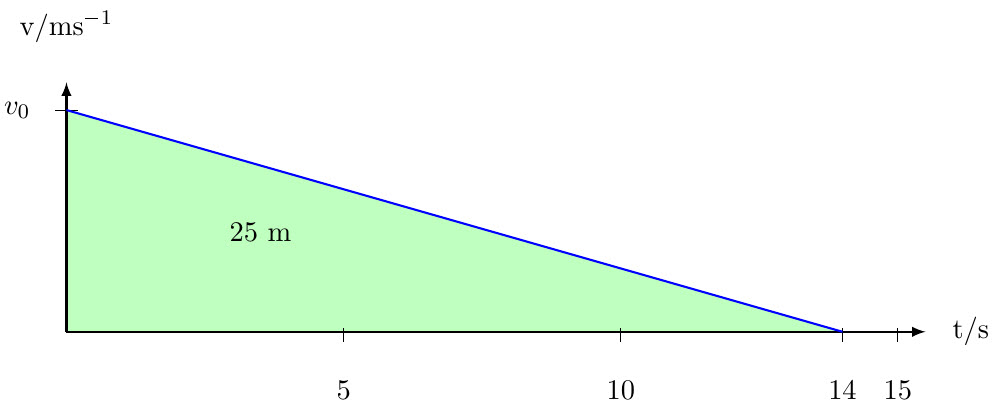 Arean motsvarar sträckan i en $vt$-graf. Alltså $\begin{align*}
25&=\dfrac{14\cdot v_0}{2} \quad \Longrightarrow \quad v_0\approx 3.6\textrm{ m/s}&&
\end{align*}$
|
|||||||||
| r-002 | En bil med hastigheten 90 km/h kör om en annan bil som håller hastigheten 72 km/h. $\textbf{(1/1/0)}$ Hur länge dröjer det innan den snabbare bilens försprång är 1 km? |
||||||||
|
|||||||||
Skillnad i hastighet mellan de båda bilarna är $90 - 72=18$ km/h $= 5$ m/s. Med denna hastighet närmar sig den bakomvarande bilen. Tiden detta tar ges av. $\begin{align*}
s&=v\cdot t &&\\
t&=\dfrac{s}{v}=\dfrac{1\,000}{5}=200 \textrm{ sekunder}&&
\end{align*}$
|
|||||||||
| r-003 | En gevärskula skjuts lodrätt uppåt. Utgångshastigheten är 240 m/s. $\textbf{(2/1/0)}$ Var befinner sig kulan 30 sekunder efter starten? Är kulan på väg uppåt eller nedåt? |
||||||||
|
|||||||||
Formeln för hastighet vid konstant acceleration. Positiv hastighet uppåt innebär att $a=-g=-9{,}82$ m/s. $\begin{align*}
v&=v_0+at&&\\
v&=240+(-9{,}82)\cdot 30=-54{,}6 \textrm{ m/s}&&
\end{align*}$
Kulan är alltså på väg nedåt. 2:a sträckformeln ger positionen vid $t=30$. $\begin{align*}
s&=v_0t+\dfrac{at^2}{2}=240\cdot 30 +\dfrac{-9{,}82\cdot 30^3}{2}=2\,781 \approx 2\,800 \textrm{ m}&&
\end{align*}$
|
|||||||||
| r-004 | En fladdermus ger ifrån sig ljud som människor inte kan höra, så kallatultraljud. $\textbf{(2/0/0)}$ Ljudet reflekteras mot ett byte och fladdermusen mottar ekot efter 0,20 s. Ljudets hastighet i luft är 340 m/s. Hur stort är avståndet till bytet? |
||||||||
|
|||||||||
Att fladdermusen mottar ekot efter 0,20 s betyder att det är tiden det tar för ljudet att färdas fram och tillbaka mellan fladdermusen och bytet, dvs. dubbla sträckan. Så det sökta avståndet ges av $\begin{align*}
s&=v\cdot t=340\cdot \dfrac{0{,}20}{2}=34 \textrm{ m}&&
\end{align*}$
|
|||||||||
| r-005 | En pojke hoppar från en bro. De sista 4 meterna innan pojken slår i vattnet tar 0,2 s.$\textbf{(0/1/2)}$ Hur hög var bron? Vi bortser från luftmotstånd.  Stari most, gamla bron över floden Neretva i Mostar. |
||||||||
|
|||||||||
Börja exempelvis med att beräkna medelhastigheten för pojken under sista 4 meterna. $\begin{align*}
\bar{v}&=\dfrac{s}{t}=\dfrac{4}{0{,}2}=20 \textrm{ m/s}&&
\end{align*}$
Sluthastigheten $v_s$ då pojken slår i vattnet blir den där medelhastigheten för de sista 4 meterna plus en likformigt accelerarad hastighet under 0,1 sekunder. 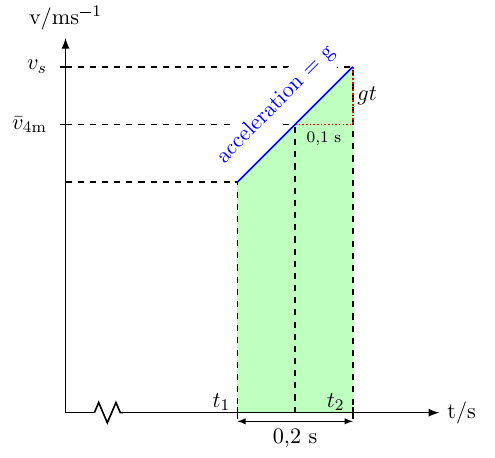 $\begin{align*}
v_s&=\bar{v}+gt=20+9{,}82\cdot 0{,}1=21 \textrm{ m/s}&&
\end{align*}$
När vi nu vet sluthastigheten $v_s$ kan falltiden $t_f$ beräknas och därefter fallhöjden. $\begin{align*}
v_s&=gt_f\quad \Longrightarrow \quad t_f=\dfrac{v_s}{g}=\dfrac{21}{9{,}82}\approx 2{,}14 \textrm{ s}&&\\
s&=\dfrac{gt_f^2}{2}=\dfrac{9{,}82\cdot 2{,}14^2}{2}=22{,}41569878\approx22\textrm{ m}&&
\end{align*}$
|
|||||||||
| r-006 | Två flygplan A och B följer samma rutt mellan två flygplatser. Det ena planet har medelhastigheten 520 km/h, det andra 650 km/h. Plan A använder 30 min kortare tid än plan B.
|
||||||||
|
|||||||||
|
|||||||||
| k-001 | Två krafter på 8,0 N respektive 5,0 N bildar vinkeln 42$^{\circ}$ med varandra. $\textbf{(1/1/0)}$ Bestäm den resulterande kraften. 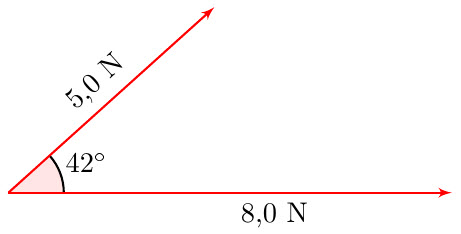 |
||||||||
|
|||||||||
Komposantuppdela 5 N kraften i $x$- respektive $y$-led och addera $x$-komposanten till 8 N kraften. Därefter pythagoras och trigonometri. $\begin{align*}
F_x&=8+5\cdot \cos 42^{\circ}&&\\[5pt]
F_y&=5\cdot \sin 42^{\circ}&&\\[5pt]
F_R&=\sqrt{F_x^2+F_y^2}=12{,}2\textrm{ N}&&\\[5pt]
v&=\arctan\left(\dfrac{F_y}{F_x}\right)=15{,}9^{\circ} &&
\end{align*}$
|
|||||||||
| k-002 | Allvarliga olyckor kan inträffa när personer åker pulka i slalombackar.$\textbf{(1/0/0)}$ Enligt ordföranden i Svenska liftanläggningars organisation kommer ett pulkaekipage i en sådan backe lätt upp i hastigheten 50 km i timmen. "Vid en kollision i den hastigheten utsätts en pulkåkare för en kraft på cirka fem ton" påstår han i en artikel i Uppsala Nya Tidning i februari 1999. Ordföranden använder ett vardagligt, "icke-fysikaliskt", sätt att uttrycka sig. Hur skulle han ha sagt för att det ska vara fysikaliskt korrekt? | ||||||||
|
|||||||||
Ett mer fysikaliskt korrekt sätt att uttrycka sig vore: ''Pulkaåkaren utsätts för kraften 50 000 N'' eller ''Pulkaåkaren utsätts för en kraft som är lika stor som tyngdkraften på massan 5 ton.'' |
|||||||||
| k-003 | Tre lika fjädrar är kopplade i serie, som i den vänstra figuren A. $\textbf{(0/1/0)}$När en tyngd hakas fast i en fästpunkt på den understa fjädern sjunker fästpunkten 6 mm. Sedan kopplar man fjädrarna som i den högra figuren B. Hur mycket sjunker då fästpunkten, när samma tyngd hakas på? |
||||||||
|
|||||||||
Varje fjäder i A förlängs alltså 2 mm. I B bär de två parallellkopplade fjädrarna halva lasten var, och förlängs därmed 1 mm. Den seriekopplade bär ju hela lasten och förlängs då precis som tidigare 2 mm. Totalt ger det 3 mm i det högra fallet. |
|||||||||
| e-001 | En kraft på 90 N som bildar vinkeln 30$^{\circ}$ mot marken drar en planka 25 m efter plan mark. $\textbf{(1/0/0)}$ Hur stort arbete uträttas av kraften? |
||||||||
|
|||||||||
Arbetet utförs av kraftkomposanten i rörelsens riktning. \begin{align*} W&=F\cdot \cos v \cdot \Delta x=90 \cdot \cos 30^{\circ} \cdot 25=1{,}95 \textrm{ kJ eller kNm}&& \end{align*} |
|||||||||
| e-002 | Anta att ett litet vattenkraftverk är lönsamt om det avger effekten
$P=700$ kW. $\textbf{(2/0/0)}$ Hur många kubikmeter vatten måste passera kraftverket varje sekund för att nå denna effekt om vattnets fallhöjd är 3,5 m och verkningsgraden är 70%? |
||||||||
|
|||||||||
Effekt är arbete/energi per tidsenhet och här behöver vi den nyttiga energin $E_{\textrm{nyttig}}=700$ kJ varje sekund för att nå lönsamhet. Ur definitionen av verkningsgrad har vi att. $\begin{align*} \eta&=\dfrac{E_{\textrm{nyttig}}}{E_{\textrm{tillförd}}} && \end{align*}$ Den tillförda energin $E_{\textrm{tillförd}}$ fås av den lägesenergi som fallhöjden ger, dvs. $\begin{align*} E_{\textrm{tillförd}}&=E_p=mgh && \end{align*}$ Vi har alltså att $\begin{align*} \dfrac{E_{\textrm{nyttig}}}{\eta}&=mgh && \end{align*}$ Lös ut massan $m$ för att beräkna hur mycket massa vatten som behöver falla per sekund. Verkningsgraden är $\eta=0{,}7$. $\begin{align*} m&= \dfrac{E_{\textrm{nyttig}}}{\eta gh} = \dfrac{700\,000}{0{,}7 \cdot 9{,}82 \cdot 3{,}5} && \\[5pt] &=29\,095 \approx 29\,000\textrm{ kg vatten per sekund}= 29 \textrm{ m$^3$ per sekund.}&& \end{align*}$ Vi antar för enkelhetens skull att 1 m$^3$ vatten väger 1 000 kg. |
|||||||||
| e-003 | En sjuksköterska styr en 75 kg tung patient liggandes på en 15 kg tung bår så att de får $\textbf{(2/0/0)}$ accelerationen 0,74 m/s$^2$. Hur stort arbete har sjuksköterskan utfört då patient och bår styrts 3,0 m? |
||||||||
|
|||||||||
Kraft och arbete ges av: $\begin{align*} F&=m\cdot a=(75+15)\cdot 0{,}74= 67\textrm{ N}&&\\[5pt] W&=F\cdot \cos v \cdot \Delta x=(75+15)\cdot 0{,}74 \cdot \cos 0^{\circ} \cdot 3=200 \textrm{ J eller Nm.}&& \end{align*}$ |
|||||||||
| e-004 | Bengt-Conny drar en låda med kraften $F=150$ N enligt figuren. Vilket arbete utför han?$\textbf{(2/0/0)}$ | ||||||||
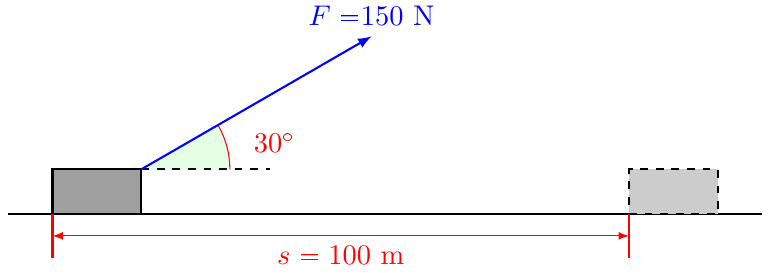 |
|||||||||
|
|||||||||
Arbetet ges av: $\begin{align*} W&=F\cdot \cos v \cdot s=150\cdot \cos 30^{\circ} \cdot 100 =12\,990 \textrm{ J eller Nm.}&& \end{align*}$ |
|||||||||
| e-005 | Hur stor effekt kan man utvinna i ett vattenkraftverk om vattenflödet$\textbf{(2/0/0)}$ är 100 m$^3$/s, fallhöjden 30 m och verkningsgraden 85%? |
||||||||
|
|||||||||
Effekt är arbete/energi per tidsenhet. Energin fås av den lägesenergi som fallhöjden ger, dvs. $E_p=mgh$. 85% av lägesenergin blir elektrisk energi, dvs. verkningsgraden är $\eta=0{,}85$. Antag att 1 kubikmeter vatten väger 1 000 kg. $\begin{align*} P_{\textrm{nyttig}}&=P_{\textrm{tillförd}}\cdot \eta =\dfrac{mgh}{t}\cdot \eta=\dfrac{100\,000\cdot 9{,}82\cdot 30\cdot 0{,}85}{1}=25\textrm{ MW} && \end{align*}$ I uppgiften står det ju redan hur mycket vatten som flödar per sekund, så tidsenheten bjuds man på här! |
|||||||||
| rm-001 | En biljardspelare stöter en biljardkula i vila med en kraft på F$=$18 N. Biljardkulan väger 0,25 kg och får hastighet $v=15$ m/s.
|
||||||||
|
|||||||||
|
|||||||||
| t-001 | Snöskor ger dig möjlighet att gå i lös snö utan att du sjunker igenom.$\textbf{(2/0/0)}$ Trycket mot snön bör dock inte överstiga 5,5 kPa för att man inte ska sjunka så djupt. Vilken är den minsta area en snösko bör ha för att du ska kunna gå i lössnö? | ||||||||
|
|||||||||
Följande samband behövs: $\begin{align*} F&=m \cdot g \quad \textrm{och}\quad p=\dfrac{F}{A}&& \end{align*}$ Antag att en person väger 75 kg $\begin{align*} A_\textrm{min}&=\dfrac{F}{p}=\dfrac{mg}{p}=\dfrac{75\cdot 9{,}82}{5\,500}=0{,}134 \textrm{ m$^2$}=13{,}4 \textrm{ dm$^2$}&& \end{align*}$ Varje sko måste ha denna area eftersom man ''står'' på ett ben i taget när man går. |
|||||||||
| tf-001 | Räkna om kokpunkten för kväve på $T_C=-196^{\circ}$C till absolut temperatur.$\textbf{(1/0/0)}$ | ||||||||
|
|||||||||
Omvandling mellan absolut temperatur $T_K$ och Celsiusgrader $T_C$ sker enligt $\begin{align*} T_K&=T_C + 273&& \end{align*}$ Svar: $T_K=-196+273=77^{\circ}$K |
|||||||||
| el-001 | En positivt laddad stav förs närmare ett positivt laddat elektroskop, utan att vidröra det.$\textbf{(2/0/0)}$ Se figur. Förklara vad som händer. 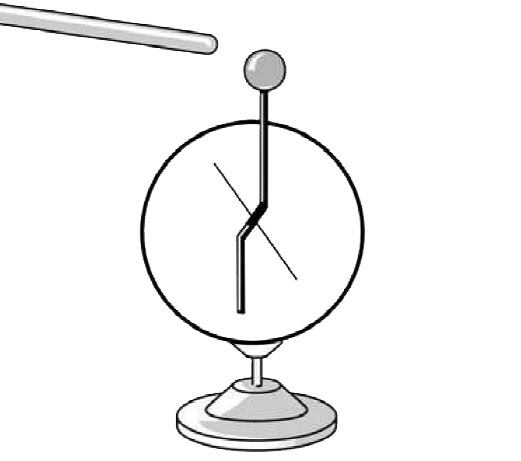 |
||||||||
|
|||||||||
Den positivt laddade staven gör att elektroner kommer att dras till elektroskopets övre del på grund av influens. Detta leder till att "visarna" kommer att få ett större underskott av elektroner varvid utslaget på elektroskopet ökar. |
|||||||||
| kf-001 | En atom sänder spontant ut en foton med energin 0,5 eV.$\textbf{(1/0/0)}$ Vilket av följande alternativ är den mest troliga förklaringen till händelsen? |
||||||||
|
|||||||||
|
|||||||||
Alternativ E
|
|||||||||
| kf-002 | Figuren nedan visar ett energinivådiagram med tre övergångar A, B och C. $\textbf{(1/1/0)}$ Övergångarna motsvarar våglängderna 103 nm, 122 nm och 656 nm. Kombinera övergångarna med rätt våglängd. |
||||||||
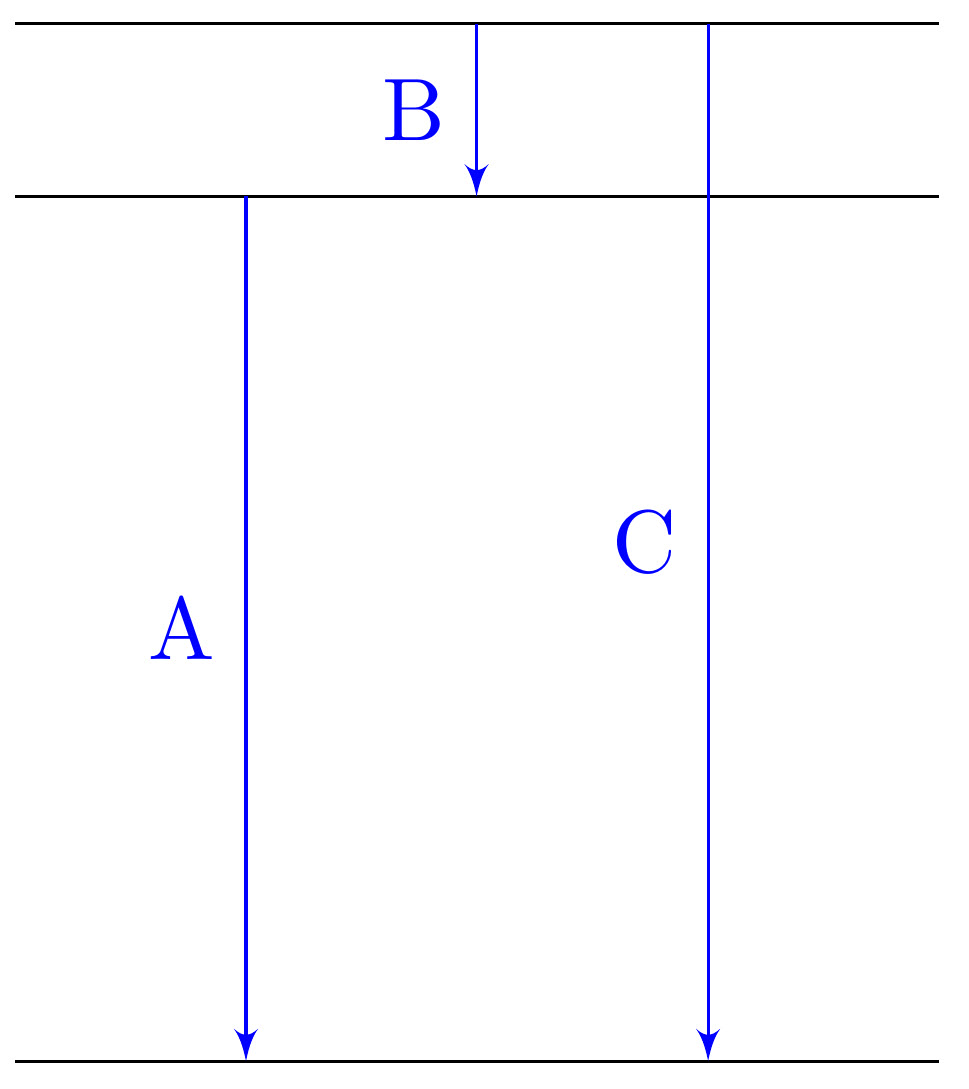 |
|||||||||
|
|||||||||
I ett energinivådiagram motsvaras längden på övergången av energin, således är den kortaste längden, B i detta fall, den övergång med lägst energi. Beräkna nu motsvarande foton-energier för övergångarna. $\begin{align*} E_{103}&=\dfrac{hc}{\lambda_{103}}=\dfrac{6{,}626\cdot 10^{-34}\cdot 299\,792\,458}{103\cdot 10^{-9}}=19{,}2\cdot 10^{-19} \textrm{ Joule}=12{,}0 \textrm{ eV}&&\\ E_{122}&=\dfrac{hc}{\lambda_{122}}=\dfrac{6{,}626\cdot 10^{-34}\cdot 299\,792\,458}{122\cdot 10^{-9}}=16{,}3\cdot 10^{-19} \textrm{ Joule}=10{,}2 \textrm{ eV}&&\\ E_{656}&=\dfrac{hc}{\lambda_{656}}=\dfrac{6{,}626\cdot 10^{-34}\cdot 299\,792\,458}{656\cdot 10^{-9}}=3{,}0\cdot 10^{-19} \textrm{ Joule}=1{,}89 \textrm{ eV}&& \end{align*}$ Alltså måste A motsvara 122 nm, B hör till 656 nm och C till 103 nm. |
|||||||||
| kf-003 | Vid dessa sänds det ut ljus med våglängderna 486 nm respektive 656 nm. $\textbf{(0/2/1)}$ Beräkna energin för nivå B. |
||||||||
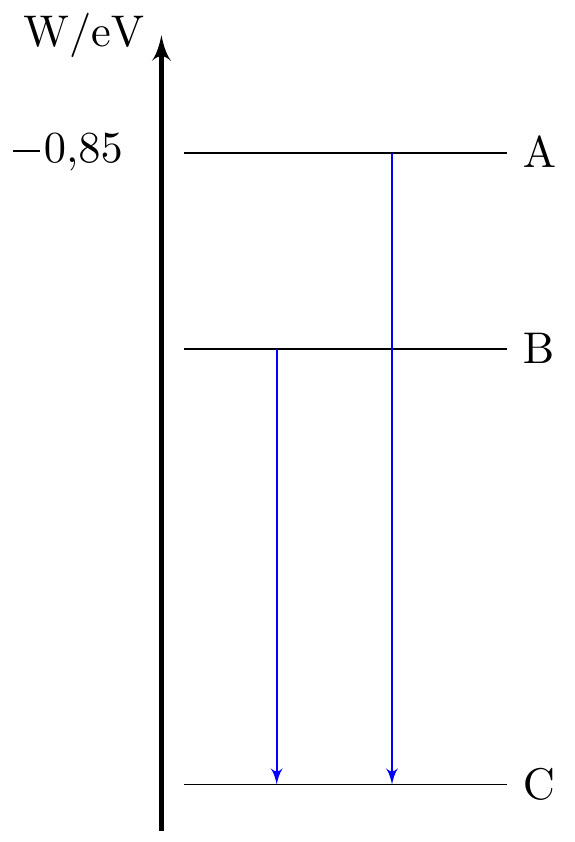 |
|||||||||
|
|||||||||
Beräkna motsvarande foton-energier för dessa båda övergångar. $\begin{align*} E_{486}&=\dfrac{hc}{\lambda_{486}}=\dfrac{6{,}626\cdot 10^{-34}\cdot 299\,792\,458}{486\cdot 10^{-9}}=4{,}1\cdot 10^{-19} \textrm{ Joule}=2{,}55 \textrm{ eV}&&\\ E_{656}&=\dfrac{hc}{\lambda_{656}}=\dfrac{6{,}626\cdot 10^{-34}\cdot 299\,792\,458}{656\cdot 10^{-9}}=3{,}0\cdot 10^{-19} \textrm{ Joule}=1{,}89 \textrm{ eV}&& \end{align*}$ Ur dessa siffror drar vi slutsatsen att övergången A$\rightarrow$C måste tillhöra våglängden 486 nm osv. Alltså fås B-nivån som $-0{,}85$ minus skillnaden mellan AC och BC $\begin{align*} \textrm{B-nivån}&=-0{,}85-(2{,}55-1{,}89)=-1{,}51 \textrm{ eV}&& \end{align*}$ |
|||||||||
| kf-004 | Figuren nedan visar en del av ett energi-nivådiagram för en atom. $\textbf{(0/2/0)}$ Energierna för de lägsta nivåerna är givna. |
||||||||
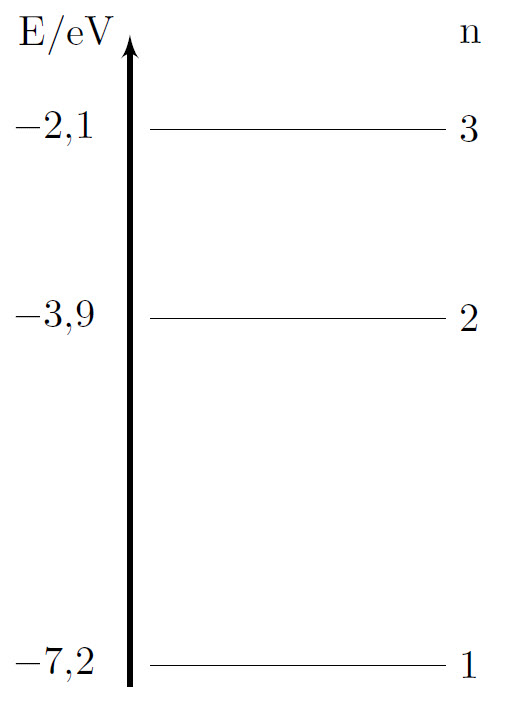 |
|||||||||
| Atomen befinner sig i sitt grundtillstånd. Beräkna våglängden för den strålning som absorberas vid excitation till nivå 2. | |||||||||
|
|||||||||
Skillnanden i energi mellan nivå 1 och 2 är $-3{,}9 - (-7{,}2)=3{,}3$ eV$=3{,}3\cdot 1{,}602\cdot 10^{-19}=5{,}29\cdot 10^{-19}$ J. 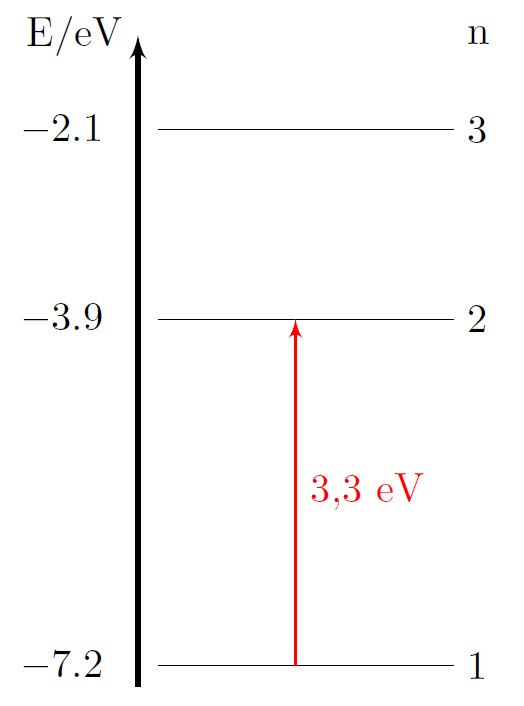 Förhållandet mellan fotonens energi och dess våglängd beskrivs av $E=\dfrac{hc}{\lambda}$ $\begin{align*} \lambda_{3{,}3}&=\dfrac{hc}{E}=\dfrac{6{,}626\cdot 10^{-34}\cdot 299\,792\,458}{5{,}29\cdot 10^{-19}}=3{,}76\cdot 10^{-7} \textrm{ m}=376 \textrm{ nm}&& \end{align*}$ Det krävs en energi motsvarande ljus med våglängden 376 nm för att excitera atomen från grundtillståndet $(n=1)$ upp till nivå 2 $(n=2)$. |
|||||||||
| kf-005 | Skriv symbolen för en nuklid med | ||||||||
|
|||||||||
|
|||||||||
|
|||||||||
| kf-006 | Medelmassan på en atom som bygger upp jorden är 40 u.$\textbf{(1/1/0)}$ Uppskatta hur många atomer det finns på jorden? |
||||||||
|
|||||||||
Jordens massa $m_{\oplus}=5{,}97 \cdot 10^{24}$ kg 1 u $=1{,}66 \cdot 10^{-27}$ kg $\begin{align*} \text{Antal atomer}=\dfrac{m_{\oplus}}{40\text{ u}}&=\dfrac{5{,}97 \cdot 10^{24}}{40 \cdot 1{,}66 \cdot 10^{-27}}=9\cdot 10^{49} \text{ stycken}&& \end{align*}$ Alltså rätt många 😊! |
|||||||||
| kf-007 | Den i naturen vanligast förekommande kolatomen har en kärna med $\textbf{(1/1/0)}$ massan 12 u och radien 3,0 fm. Beräkna kärnans densitet. |
||||||||
|
|||||||||
Densiteten kan beräknas om vi vet massan och volymen för $\ce{^{12}_{6}C}$. Massan fås ur $\begin{align*} m\left(\ce{^{12}_{6}C}\right)=&12\cdot 1{,}66 \cdot 10^{-27}=1{,}99 \cdot 10^{-26}\textrm{ kg}&& \end{align*}$ Volymen för kolatomen ges av $\begin{align*} V\left(\ce{^{12}_{6}C}\right)=&\dfrac{4\pi r^3}{3}=\dfrac{4\pi \left(3{,}0 \cdot 10^{-15}\right)^3}{3}=1{,}13 \cdot 10^{-43}\textrm{ kg}&&\end{align*}$ Densiteten blir $\begin{align*} \varrho\left(\ce{^{12}_{6}C}\right)=&\dfrac{m}{V}=\dfrac{1{,}99 \cdot 10^{-26}}{1{,}13 \cdot 10^{-43}}=1{,}76 \cdot 10^{17} \textrm{ kg/m$^3$}&& \end{align*}$ Jämfört med guld som har densiteten $\varrho=19\,300$ kg/m$^3$. Guld är ett av de tätaste grundämnena på jorden! Kolkärnan är ungefär 14 storleksorningar tätare. Eller uttryckt såhär, en vanlig speltärning gjord av endast atomkärnmaterial skulle väga ungefär 175 miljoner ton! Det är ungefär 1000 fullastade supertankers! |
|||||||||
| kf-008 | Ange antalet elektroner, protoner och neutroner i en atom av nukliderna nedan. | ||||||||
|
|||||||||
|
|||||||||
|
|||||||||
| kf-009 | Energin som frigörs från solen orsakas av kärnprocesser i solens inre. Väte omvandlas till$\textbf{(1/0/0)}$ helium. Du kan som en förenklad reaktionsmekanism tänka dig att två protoner och två neutroner bildar en heliumkärna. Varför frigörs energi vid denna process? Vilket av följande alternativ är det rätta? |
||||||||
|
|||||||||
|
|||||||||
B) Massan hos heliumkärnan är mindre än den sammanlagda massan av protonerna och neutronerna och därför frigörs energi när heliumkärnan bildas. |
|||||||||
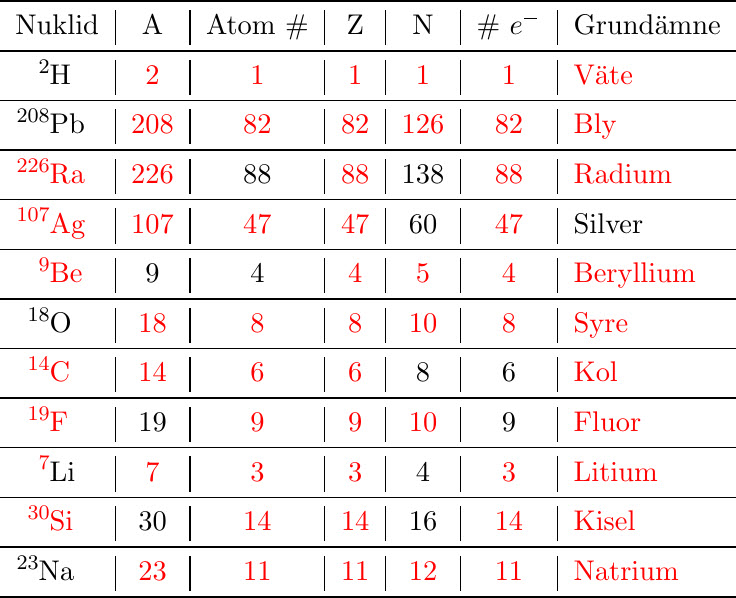
| kf-010 | Fyll i tabellen nedan!$\textbf{(1/0/0)}$ | ||||||||
 |
|||||||||
|
|||||||||
 |
|||||||||
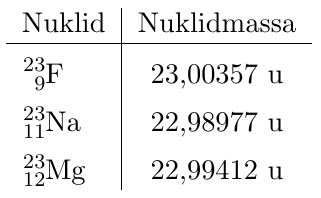
| kf-011 | Nedan finns angivet tre stycken nuklider som har masstalet 23. $\textbf{(0/2/1)}$ Beräkna bindningsenergin/nukleon för dessa tre nuklider. Vilken slutsats kan du dra av dina beräkningar? |
||||||||
 |
|||||||||
|
|||||||||
Bindningsenergin för en nuklid beräknas som skillnaden mellan summan av de fria partiklarnas massa och det bundna tillståndet. Man får bindningsenergin per nukleon för de tre nukliderna enligt. $\begin{align*} \ce{^{23}_{9}F}=&\dfrac{\left(9\cdot 5{,}4858 \cdot 10^{-4}+9 \cdot 1{,}007276+14 \cdot 1{,}008665-23{,}00357\right)\cdot 931{,}49}{23}&&\\ =&7{,}62\textrm{ MeV/nukleon}&&\\ \phantom{a} \\ \ce{^{23}_{11}Na}=&\dfrac{\left(11\cdot 5{,}4858 \cdot 10^{-4}+11 \cdot 1{,}007276+12 \cdot 1{,}008665-22{,}98977\right)\cdot 931{,}49}{23}&&\\ =&8{,}11\textrm{ MeV/nukleon}&&\\ \phantom{a} \\ \ce{^{23}_{12}Mg}=&\dfrac{\left(12\cdot 5{,}4858 \cdot 10^{-4}+12 \cdot 1{,}007276+11 \cdot 1{,}008665-22{,}99412\right)\cdot 931{,}49}{23}&&\\ =&7{,}90\textrm{ MeV/nukleon}&& \end{align*}$ Slutsats: Natrium är mest stabil och Fluor minst stabil. |
|||||||||
| kf-012 | Uranisotopen $\ce{^{232}_{92}U}$ sönderfaller genom att sända ut alfapartiklar.$\textbf{(1/0/0)}$ Ange kemisk beteckning, atomnummer och masstal för dotterkärnan. |
||||||||
|
|||||||||
Sönderfallet blir enligt $\ce{^{232}_{92}U} \ce{ -> } \ce{^{228}_{90}Th} + \ce{^{4}_{2}He}$ Dotterkärnan: Isotopen med masstalet 228 av grundämnet Thorium-90 |
|||||||||
| kf-013 | Uranisotopen $\ce{^{238}_{92}U}$ kan fånga in en neutron. Den kärna som bildas
är instabil och genomgår$\textbf{(1/0/0)}$ två stycken betasönderfall ($\beta^-$). Bestäm slutprodukten och dess masstal. |
||||||||
|
|||||||||
Sönderfallet blir enligt $\begin{align*} \ce{^{238}_{92}U} + \ce{^{1}_{0}n} \ce{ -> }& \ce{^{239}_{92}U} &&\\ \ce{^{239}_{92}U} \ce{ -> }& \ce{^{239}_{93}Np} + \ce{^{0}_{-1}e} + \ce{^{}_{}\bar{\nu}_e}&&\\ \ce{^{239}_{93}Np} \ce{ -> }& \ce{^{239}_{94}Pu} + \ce{^{0}_{-1}e} + \ce{^{}_{}\bar{\nu}_e}&& \end{align*}$ Slutprodukt: Plutonium $\ce{^{239}_{94}Pu}$ |
|||||||||
| kf-014 | Bestäm partikeln X i följande kärnreaktioner | ||||||||
| |||||||||
|
|||||||||
|
|||||||||
| kf-015 | Svara på följande frågeställningar om massenergi | ||||||||
|
|||||||||
|
|||||||||
|
|||||||||
| kf-016 | Vi sänder alfapartiklar, var och en med kinetiska energin $8{,}0\cdot 10^{-13}$ J, in mot en folie av bor. När alfapartiklarna träffar folien kan det sändas ut neutroner från folien. | ||||||||
|
|||||||||
|
|||||||||
|
|||||||||
| kf-017 | En kärnreaktion kan gå till på följande sätt: $\textbf{(1/2/0)}$ $\gamma + \ce{^{2}_{1}H} \ce{ -> } \ce{^{1}_{1}H} + \ce{^{1}_{0}n}$ Vad händer i denna reaktion? Hur stor energi måste gammakvantat minst ha för att reaktionen ska ske? |
||||||||
|
|||||||||
En gammafoton slår loss en neutron ur en deuteriumkärna (tungt väte $\ce{^{2}_{1}H}$). Vi sätter upp före minus efter för energin och bestämmer gränsen, här kallad $x$, för hur stor energi som gammafotonen måste ha. $\begin{align*}
\Delta m&=\color{red}\Big(\color{black} x+ m\left(\ce{^{2}_{1}H}\right) \color{red}\Big)\color{black} - \color{red}\Big(\color{black}m\left(\ce{^{1}_{1}H}\right) + m\left(\ce{^{1}_{0}n} \right)\color{red}\Big)\color{black} =0 &&
\end{align*}$
OBS! Ingen svag växelverkan, alltså inget proton/neutron sönderfall, i denna kärnreaktion. Det betyder att vi har ett nollsummespel mellan elektronerna och lika många före som efter! Ta nuklidmassorna ur tabellen och lös ut $x$ och omvandla till lämpliga enheter. $\begin{align*}
x&=m\left(\ce{^{1}_{1}H}\right) + m\left(\ce{^{1}_{0}n}\right) - m\left(\ce{^{2}_{1}H}\right) &&\\[5pt]
x&=1{,}007825032 + 1{,}0086649- 2{,}01410177 = 0{,}002388162 \textrm{ u} &&\\[5pt]
&= 0{,}002388162 \cdot 931{,}49 = 2{,}224549\textrm{ MeV} \approx 2{,}2 \textrm{ MeV} &&\\[5pt]
&=2{,}224549\cdot 10^6 \cdot 1,602\cdot 10^{-19} \approx 3,6\cdot 10^{-13} \textrm{ J}&&
\end{align*}$
|
|||||||||
| kf-018 | Vi tänker oss att vi ska skapa en neutral $\ce{^{7}_{}Li}$-atom av fria protoner, neutroner och elektroner.
|
||||||||
|
|||||||||
|
|||||||||
| kf-019 | Den radioaktiva nukliden $\ce{^{198}_{}Au}$ kan genom betastrålning omvandlas till $\ce{^{198}_{}Hg}$ på tre olika sätt. Se figuren. När kärnan bildas i grundtillståndet, får betapartiklarna energin $2{,}19\cdot 10^{-13}$ J.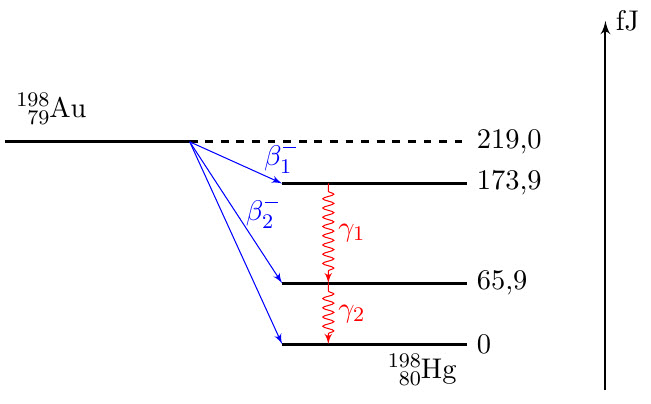
|
||||||||
|
|||||||||
|
|||||||||
| kf-020 | Atomkärnan $\ce{^{235}_{92}U}$ träffas av en neutron. Då bildas två nya, likadana kärnor och två neutroner sänds ut.
|
||||||||
|
|||||||||
|
|||||||||
| kf-021 | Energiproduktionen i Solen sker till största delen genom den så kallade proton-proton fusionen. Förenklat kan den sammanfattas med reaktionen $\begin{equation*} 4\left(\ce{^{1}_{1}H}\right) + 2 \left(\ce{^{0}_{-1}e^-}\right) \ce{ -> } \ce{^{4}_{2}He} + 2\ce{\nu_e} + \textrm{Energi} \end{equation*}$ |
||||||||
På en sekund utstrålar Solen energin $3{,}9\cdot 10^{26}$ J. |
|||||||||
|
|||||||||
|
|||||||||
| kf-022 | Beräkna den frigjorda massenergin när ett halvt gram materia$\textbf{(2/0/0)}$ och ett halvt gram antimateria annihilerar varandra. |
||||||||
|
|||||||||
Energin ges direkt av $\begin{align*}
E &=(0{,}0005+0{,}0005)\cdot (3\cdot 10^8)^2=9{,}0\cdot 10^{13} \textrm{ J}&&
\end{align*}$
|
|||||||||
| kf-023 | Ett ämnesprov innehållande Thorium träffas av neutroner. Svara på följande frågor.
|
||||||||
 |
|||||||||
|
|||||||||
|
|||||||||
| kf-024 | Bestäm masstal och atomnummer för slutkärnan om kärnan $\ce{^{A}_{B}X}$ sönderfaller med
|
||||||||
|
|||||||||
|
|||||||||
| kf-025 | Komplettera reaktionsformeln $\ce{X} + \ce{^{4}_{2}He} \ce{ -> } \ce{^{16}_{8}O} $ $\textbf{(1/0/0)}$ | ||||||||
|
|||||||||
Bevarandelagarna för kärnreaktioner ger att $\begin{align*}
\ce{^{12}_{6}C} + \ce{^{4}_{2}He} \ce{ -> }& \ce{^{16}_{8}O}&&
\end{align*}$
Den okända kärnan är kol-12 $\ce{^{12}_{6}C}$ som tar upp en alfa-partikel och bildar syre-16. |
|||||||||
| kf-026 | Isotopen $\ce{^{64}_{29}Cu}$ är ovanlig då den kan sönderfalla både med
$\gamma$-, $\beta^-$- och $\beta^+$-sönderfall.$\textbf{(2/0/0)}$ Vilken är slutkärnan i de olika fallen? Skriv upp de olika reaktionsforrnlerna. |
||||||||
|
|||||||||
Sönderfallen blir enligt $\begin{align*} \ce{^{64}_{29}Cu} \ce{ -> }& \ce{^{64}_{29}Cu} && \gamma\\[5pt] \ce{^{64}_{29}Cu} \ce{ -> }& \ce{^{64}_{30}Zn} + \ce{^{0}_{-1}e} + \ce{^{}_{}\bar{\nu}_e}&&\beta^-\\[5pt] \ce{^{64}_{29}Cu} \ce{ -> }& \ce{^{64}_{28}Ni} + \ce{^{0}_{+1}e} + \ce{^{}_{}\nu_e}&&\beta^+ \end{align*}$ |
|||||||||
| kf-027 | Nukliden $\ce{^{210}_{84}Po}$ är alfastrålare. Skriv formeln för dess sönderfall.$\textbf{(1/0/0)}$ | ||||||||
|
|||||||||
Sönderfallen blir enligt $\begin{equation*}
\ce{^{210}_{84}Po} \ce{ -> } \ce{^{206}_{82}Pb} + \ce{^{4}_{2}He}
\end{equation*}$
Not. Ett gram av grundämnet polonium-210 kan i teorin döda omkring 10 miljoner människor, dessutom är det ett ämne som är svårt att upptäcka. Ämnet förekommer i naturen i små mängder överallt omkring oss och är helt ofarligt. Det blir farligt först om det hamnar i vår mat. Enligt schweiziska forskare dödades Yasser Arafat med 83 procents sannolikhet av poloniumförgiftning, de hittade ämnet i kvarlevor som 2012 grävdes upp ur Yassir Arafats grav i Ramallah på den ockuperade Västbanken. Ämnet upptäcktes 1898 av Marie Curie och fick namn efter hennes hemland (Polen). Det var det första radioaktiva ämnet som upptäcktes. |
|||||||||
| kf-028 | Genom en serie av sönderfall övergår $\ce{^{235}_{92}U}$ till $\ce{^{207}_{82}Pb}$.$\textbf{(1/1/0)}$ Hur många $\alpha-$ och $\beta-$partiklar emitteras i den här sönderfallsserien? |
||||||||
|
|||||||||
$\alpha$-sönderfallet minskar masstalet med 4 och och laddningen med 2 och $\beta$-sönderfallet antingen ökar eller minskar laddningen med 1. Vi kan då ställa upp ett ekvationssystem för att lösa uppgiften. $\begin{align*} \left\{\begin{aligned} 235-4\alpha \color{pink!20}+\beta\color{black} &= 207 \\ 92\color{pink!20}5\color{black} - 2\alpha + \beta &= 82 \end{aligned}\right. \quad \Longrightarrow \quad \left\{\begin{aligned} \alpha &= 7 \\ \beta &= 4 \end{aligned}\right. \end{align*}$ Vi ser att $\beta$ är positivt 4, det betyder alltså att laddningen ökat med 4 och att det varit fråga om 4 stycken $\beta^-$-sönderfall. Den så kallade actinium-serien är en serie sönderfall som startar med $\ce{^{235}_{92}U}$ och slutar med $\ce{^{207}_{82}Pb}$. Jag hittade den här utmärkta illustrationen över hur sönderfallet sker på wikipedia. 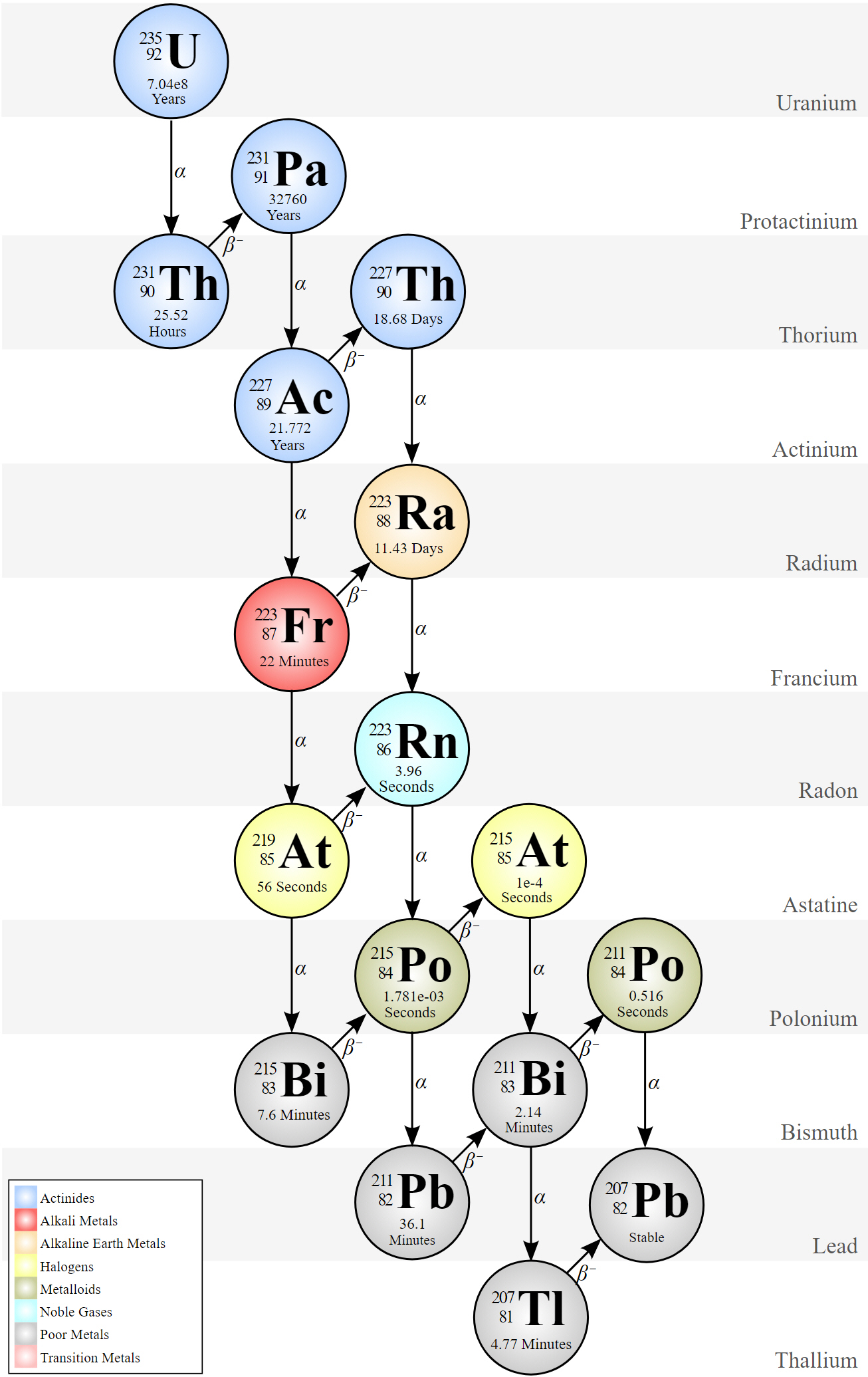 Följer man de olika vägarna ser man att det krävs 7 $\alpha$-sönderfall och 4 $\beta^-$-sönderfall för att nå slutkärnan $\ce{^{207}_{82}Pb}$. |
|||||||||
| kf-029 | Beräkna för nukliden $\ce{^{58}_{28}Ni}$
|
||||||||
|
|||||||||
|
|||||||||
| kf-030 | Nukliden $\ce{^{32}_{15}P}$ sönderfaller genom att sända ut en elektron, vars maximala kinetiska energi är 1,71 MeV.
|
||||||||
|
|||||||||
|
|||||||||
| kf-031 | $\ce{^{18}_{}F}$ sönderfaller med betasönderfall till $\ce{^{18}_{}O}$.
|
||||||||
|
|||||||||
|
|||||||||
| kf-032 | Bindningsenergin för nukliden $\ce{^{16}_{8}O}$ är 127,6 MeV. Beräkna dess nuklidmassa.$\textbf{(1/2/0)}$ | ||||||||
|
|||||||||
Ur vår tabell kan vi avläsa detta direkt enligt $m\left(\ce{^{16}_{8}O}\right)=15{,}9949146196 \textrm{ u}$! Men tanken här är att vi skall beräkna summan av de fria partiklarnas massa och sedan subtrahera bindningsenergin omvandlad till massa. Summan av nukleonernas och elektronernas massor blir. $\begin{equation*}
m(n+p+ e^-)=8\cdot 5{,}4858 \cdot 10^{-4} + 8 \cdot 1{,}007276 +8 \cdot 1{,}008665 = 16{,}13191664\textrm{ u}
\end{equation*}$
Bindningsenergin 127,6 MeV motsvarar massan $\dfrac{127{,}6}{931{,}49}=0{,}13698483$ u. Så nuklidmassan blir då. $\begin{equation*}
m\left(\ce{^{16}_{8}O}\right)=16{,}13191664 - 0{,}13698483= 15{,}99493181 \textrm{ u}
\end{equation*}$
Det skiljer sig åt i 5:e decimalen och detta beror återigen på att bindningsenergin har dålig noggranhet. |
|||||||||
| kf-033 | Bestäm hur mycket energi man får ur denna reaktion.$\textbf{(1/1/0)}$ $\begin{equation*}
\ce{p} + \ce{^{7}_{3}Li} \ce{ -> } \ce{^{4}_{2}He} + \ce{^{4}_{2}He}
\end{equation*}$ |
||||||||
|
|||||||||
Kort och gott, energin före minus energin efter, men kom ihåg att det är kärnorna som reagerar och i just denna reaktion så lägger ni märke till att vi har en ojämvikt mellan antalet elektroner före och efter. Så när vi plockar nuklidmassorna ur tabellen (alltså inklusive elektronerna) måste vi kompensera för dessa elektronmassor. $\begin{align*}
\Delta m&=\color{red}\Big(\color{black}m(\ce{p}) + m\left(\ce{^{7}_{3}Li}\right) - 3\cdot m(\ce{^{}_{}e^-})\color{red}\Big)\color{black} - \color{red}\Big(\color{black}2\cdot m\left(\ce{^{4}_{2}He}\right) - 4\cdot m(\ce{^{}_{}e^-}) \color{red}\Big)\color{black} &&\\
&=\color{red}\Big(\color{black}1{,}007276+7{,}01600344 - 3\cdot 0{,}00054858\color{red}\Big)\color{black}&&\\
&\phantom{=} - \color{red}\Big(\color{black} 2\cdot 4{,}0026032541- 4\cdot 0{,}00054858\color{red}\Big)\color{black} &&\\
&=8{,}0216337 - 8{,}003012188 = 0{,}018621512 \textrm{ u} &&
\end{align*}$
energiutbytet blir då $\begin{equation*}
\Delta E=0{,}018621512 \cdot 931{,}49\approx 17{,}3 \textrm{ MeV} \quad \quad (17{,}345566)
\end{equation*}$
|
|||||||||
| kf-034 | Väteisotopen $\ce{^{3}_{1}H}$ är instabil och sönderfaller med betasönderfall.
|
||||||||
|
|||||||||
|
|||||||||
| kf-035 | Huvuddelen (94,6%) av kärnorna i ett $\ce{^{137}_{55}Cs}$-preparat sönderfaller till en exciterad nivå i dotterkärnan enligt figuren.
|
||||||||
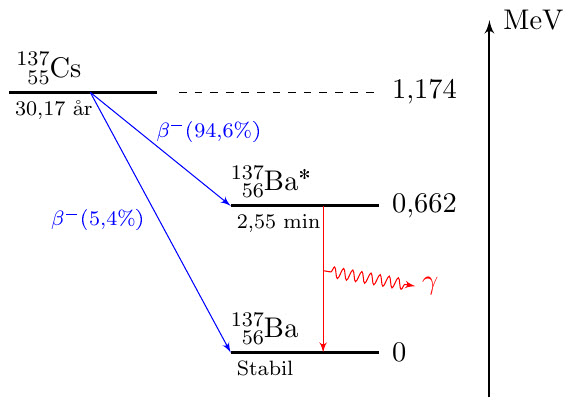 |
|||||||||
|
|||||||||
|
|||||||||
| kf-036 | Nukliden $\ce{^{6}_{3}Li}$ beskjuts med deutroner ($\ce{^{2}_{1}H}$) varvid 2 stycken $\ce{^{4}_{2}He}$ bildas.
|
||||||||
|
|||||||||
|
|||||||||
| kf-037 | Då $\ce{^{235}_{92}U}$ bestrålas med så kallade termiska neutroner kan en fission erhållas. En av många tänkbara klyvningsprocesser är följande: $\begin{equation*}
\ce{^{235}_{92}U} + \ce{^{1}_{0}n} \ce{ -> } \ce{^{89}_{36}Kr} + \ce{^{A}_{Z}X} + 3\cdot \ce{^{1}_{0}n}
\end{equation*}$
|
||||||||
|
|||||||||
|
|||||||||
| kf-038 | Uranisotopen $\ce{^{234}_{92}U}$ sönderfaller genom att sända ut alfapartiklar enligt$\textbf{(1/2/0)}$ $\begin{equation*}
\ce{^{234}_{92}U} \ce{ -> } \ce{^{230}_{90}Th} + \ce{^{4}_{2}He}
\end{equation*}$
Vilken rörelseenergi får alfapartikeln om uran- och thoriumkärnorna kan bektraktas vara i vila? |
||||||||
|
|||||||||
Massdefekten beräknas enkelt som skillnaden mellan nuklidmassorna före och efter. $\begin{align*}
\Delta m&= m\left(\ce{^{234}_{92}U}\right) - m\left(\ce{^{230}_{90}Th} \right) - m\left(\ce{^{4}_{2}He}\right) &&\\[5pt]
&= 234{,}0409504 - 230{,}0331324 - 4{,}0026032541 = 0{,}0052147459 \textrm{ u}&&
\end{align*}$
Uttryckt i energi blir detta $\begin{align*}
E&= 0{,}0052147459 \cdot 931{,}49 = 4{,}86 \textrm{ MeV}&&
\end{align*}$
|
|||||||||
| kf-039 | Efter kärnkraftsolyckan i Tjernobyl 1986 spreds bland annat den radioaktiva isotopen $\ce{^{137}_{55}Cs}$ i vissa delar av Sverige.
|
||||||||
|
|||||||||
|
|||||||||
| kf-040 | Radioaktivt jod med halveringstiden 25 minuter används ofta inom sjukvården för $\textbf{(1/0/0)}$ diagnostisering. Hur stor del av ett preparats aktivitet finns kvar efter 1 h och 40 min? |
||||||||
|
|||||||||
Aktiviteten kan beräknas direkt ur sönderfallsformeln. $\begin{align*}
A=& A_0\cdot \left(\dfrac{1}{2}\right)^{\dfrac{t}{T_{1/2}}}=A_0\cdot \left(\dfrac{1}{2}\right)^{\dfrac{100}{25}}=0{,}0625A_0&&
\end{align*}$
Det finns 6,25% kvar. |
|||||||||
| kf-041 | Två preparat A och B, består av samma radioaktiva nuklid. $\textbf{(1/0/0)}$ Preparat A har dubbelt så stor aktivitet som preparat B. Hur är detta möjligt? |
||||||||
|
|||||||||
Aktiviteten beror också på hur mycket av ämnet man har och förklaringen är då att det helt enkelt finns dubbelt så mycket av preparat A. Preparatet A väger dubbelt så mycket som preparat B. Det skulle också kunna bero på att preparat B har färdigställt vid en tidigare tidpunkt och därmed har halverats när jämförelsen startar. |
|||||||||
| kf-042 | Med en detektor (geigerräknare) registrerar vi strålningen från en radioaktiv källa. Resultatet har införts i tabellen. 
|
||||||||
|
|||||||||
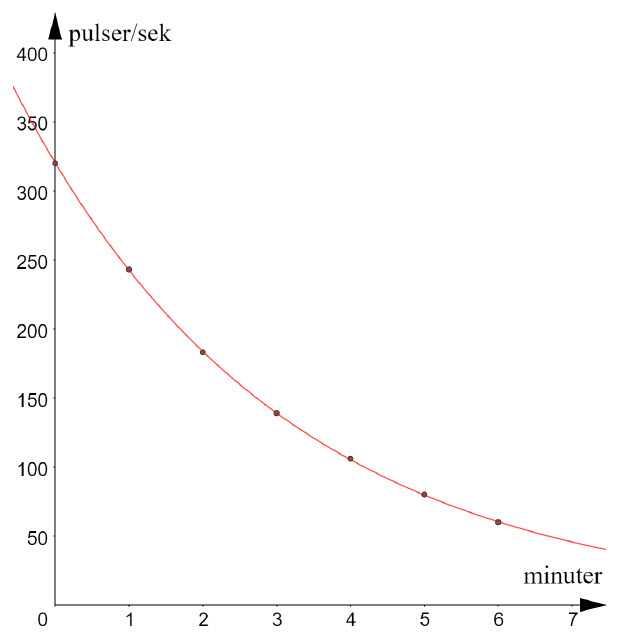
|
|||||||||
| kf-043 | I Amenhotep III´s grav har man hittat en mumie vars innehåll av kol-14 år 1980 uppmättes till 65,5% av det normala innehållet i levande material.
|
||||||||
|
|||||||||
|
|||||||||
| kf-044 | Luften i ett källarrum innehåller den radioaktiva gasen radon-222. Radonet sipprar in i$\textbf{(0/1/0)}$ rummet genom golvet och väggarna. När rummet inte luftas, visar mätningar att aktiviteten från radongasen håller sig konstant lika med 200 Bq/m$^3$. Källarrummets volym är 130 m$^3$. Hur många radonatomer sipprar in i källar-rummet varje sekund? |
||||||||
|
|||||||||
Om aktiviteten är konstant måste det tillkomma lika många radonatomer som det sönderfaller! 200 Bq/m$^3$ ger $200\cdot 130 = 26\,000$ Bq totalt i källaren. |
|||||||||
| kf-045 | I ett prov finns det till att börja med $3{,}2\cdot 10^{16}$ kärnor av ett visst radioaktivt ämne.$\textbf{(0/1/0)}$ Halveringstiden är 45 min. Vid varje radioaktiv omvandling frigörs $5{,}0\cdot 10^{-13}$ J. Hur stor energi har totalt frigjorts under 3,0 timmar? |
||||||||
|
|||||||||
Vi konstaterar att 3h i denna uppgift motsvarar exakt 4 halveringstider á 45 minuter. Det betyder alltså att antalet kärnor har minskat med en faktor $16=2^4$. Antal kärnor som sönderfallit blir då $\begin{align*}
N&=3{,}2\cdot 10^{16}-\dfrac{3{,}2\cdot 10^{16}}{16}=3{,}0\cdot 10^{16} \textrm{ stycken} &&
\end{align*}$ Den frigjorda energin blir $\begin{align*} E&=3{,}0\cdot 10^{16} \cdot 5{,}0\cdot 10^{-13}= 15\,000 \textrm{ J} && \end{align*}$ |
|||||||||
| kf-046 | Du har 414 gram av den radioaktiva isotopen Radon-220 $\ce{^{220}_{86}Rn}$. $\textbf{(0/2/1)}$ Efter hur lång tid finns endast 95,5 gram kvar? |
||||||||
|
|||||||||
Ur tabellen hittar man halveringstiden för $\ce{^{220}_{86}Rn}$ till $T_{1/2}=55{,}6$ sekunder. Sönderfallsformeln ger då $\begin{align*}
m&= m_0\cdot \left(\dfrac{1}{2}\right)^{\dfrac{t}{T_{1/2}}} \quad \Longrightarrow \quad 95{,}5= 414\cdot \left(\dfrac{1}{2}\right)^{\dfrac{t}{55{,}6}}&&
\end{align*}$
För att komma åt tiden $t$ behöver man logaritmera, jag brukar alltid använda den naturliga logaritmen, men det spelar ingen roll om ni hellre vill använda 10-logaritmen! Man får. $\begin{align*}
\ln\left(\dfrac{95{,}5}{414}\right)&= \ln\left(\left(\dfrac{1}{2}\right)^{\dfrac{t}{55{,}6}}\right)=\dfrac{t}{55{,}6}\cdot \ln\left(\dfrac{1}{2}\right)&&
\end{align*}$
Lös ut $t$ på vanligt sätt. $\begin{align*}
t&= \dfrac{55{,}6\cdot \ln\left(\dfrac{95{,}5}{414}\right)}{\ln\left(\dfrac{1}{2}\right)}=117{,}65 \approx 118\textrm{ sekunder}&&
\end{align*}$ |
|||||||||
| kf-047 | Ett milligram aktinium innehåller $2{,}66\cdot 10^{18}$ atomer och aktiviteten
är $4{,}34\cdot 10^9$ Bq. $\textbf{(1/1/1)}$ Beräkna aktiniums sönderfallskonstant och halveringstid. |
||||||||
|
|||||||||
Aktiviteten är definierad enligt $A=\lambda \cdot N$. Ur detta beräknar vi sönderfallskonstanten för aktinium. $\begin{align*}
A&= \lambda \cdot N \quad \Longrightarrow \quad \lambda = \dfrac{4{,}34\cdot 10^9}{2{,}66\cdot 10^{18}}=1{,}63\cdot 10^{-9}\textrm{ per sekund}&&
\end{align*}$
Halveringstiden förhåller sig till sönderfallskonstanten enligt. $\begin{align*}
T_{1/2}&=\dfrac{\ln2}{\lambda}=\dfrac{\ln2}{1{,}63\cdot 10^{-9}}=424\,832\,143\textrm{ sekunder}\approx 13{,}5\textrm{ år}&&
\end{align*}$ |
|||||||||
| kf-048 | Efter 7,57 år innehåller ett radioaktivt preparat 84% av den ursprungliga mängden $\textbf{(0/2/1)}$ radioaktiv nuklid. Hur lång är halveringstiden för denna radioaktiva nuklid? Vilken nuklid kan det röra sig om? |
||||||||
|
|||||||||
Sönderfallsformeln ger i detta fall $\begin{align*}
N&= N_0\cdot \left(\dfrac{1}{2}\right)^{\dfrac{t}{T_{1/2}}} \quad \Longrightarrow \quad 0{,}84N_0=N_0\cdot \left(\dfrac{1}{2}\right)^{\dfrac{7{,}57}{T_{1/2}}}&&
\end{align*}$
Dividera bort $N_0$ och logaritmera! $\begin{align*}
\ln(0{,}84)&=\ln\left(\left(\dfrac{1}{2}\right)^{\dfrac{7{,}57}{T_{1/2}}}\right)=\dfrac{7{,}57}{T_{1/2}}\ln\left(\dfrac{1}{2}\right)&&
\end{align*}$
$T_{1/2}$ fås nu som $\begin{align*}
T_{1/2}&=\dfrac{7{,}57\cdot\ln\left(\dfrac{1}{2}\right)}{\ln(0{,}84)}=30{,}1 \textrm{ år} &&
\end{align*}$
$T_{1/2}=30{,}1$ år, det stämmer bra för nukliden $\ce{^{137}_{55}Cs}$. |
|||||||||
| kf-049 | I ett skåp på fysikinstitutionen hittar man ett gammalt strontiumpreparat $\ce{^{90}_{38}Sr}$ som är $\textbf{(1/1/1)}$ 14 år gammalt. Ett mätprotokoll visar att man då uppmätte aktiviteten 2 780 pulser/min vid en bakgrundsstrålning på 210 pulser/minut. Hur många pulser/min bör man uppmäta idag, om bakgrundsstrålningen är densamma? |
||||||||
|
|||||||||
Halveringstiden för $\ce{^{90}_{38}Sr}$ är $T_{1/2}=29$ år. Antal pulser/min för 14 år sedan blir $2\,780 - 210 = 2\,570$ pulser/min. Antalet pulser idag, 14 år senare, fås enligt. (Jag kallar detta A, det är ju en aktivitet). $\begin{align*}
A=& A_0\cdot \left(\dfrac{1}{2}\right)^{\dfrac{t}{T_{1/2}}}=2\,570\cdot \left(\dfrac{1}{2}\right)^{\dfrac{14}{29}}=1\,839\textrm{ pulser/min}&&
\end{align*}$
Bakgrundsstrålningen är densamma så man bör uppmäta $1\,839 + 210 = 2\,049 \approx 2\,050$ pulser/min. |
|||||||||
| kf-050 | Du tänker göra te genom att värma vatten genom att låta det absorbera röntgenstrålning. $\textbf{(1/1/1)}$ Hur lång tid tar det att höja temperaturen hos en kopp vatten från 10$^{\circ}$C till 85$^{\circ}$C med hjälp av röntgenstrålning från en maskin som producerar 1,0 mGy varje sekund? 1,0 mGy är den dos som absorberas vid en genomsnittlig röntgenundersökning. |
||||||||
|
|||||||||
Antag att en kopp med vatten innehåller ungefär 2,5 dl, vilket väger $m=0{,}25$ kg. Vattnets specifika värmekapacitet är 4\,180 J/kg$\cdot$K. Då får vi den nödvändiga energimängden för uppvärminingen. $\begin{align*}
E=& mc\Delta T=0{,}25\cdot 4\,180 \cdot 75=78\,375 \textrm{ J}&&
\end{align*}$
Röntgenstrålningen från maskinen avger $E=D\cdot m=0{,}001\cdot 0{,}25=0{,}00025$ J varje sekund. Det kommer alltså att krävas $\begin{align*}
t=& \dfrac{78\,375}{0{,}00025}=9{,}9 \textrm{ år!!!} &&
\end{align*}$
Ingen vidare bra metod! |
|||||||||
| kf-051 | En person som väger 85 kg absorberar dosen 0,25 Gy jämnt över hela kroppen. $\textbf{(1/0/0)}$ Hur mycket energi tillför detta kroppen? |
||||||||
|
|||||||||
Den absorberade stråldosen $D$ förhåller sig till tillförd energi enligt $\begin{align*}
D=& \dfrac{E}{m} \quad \Longrightarrow \quad E=D\cdot m= 0{,}25 \cdot 85 = 21{,}25\textrm{ Joule}&&
\end{align*}$ |
|||||||||
| kf-052 | Samma person som i föregående uppgift, dvs. en person som väger 85 kg, $\textbf{(1/1/0)}$ exponeras nu för den ekvivalenta dosen 3,5 mSv i form av $\alpha$-strålning. Hur mycket energi absorberar personen nu? |
||||||||
|
|||||||||
Den ekvivalenta dosen $H=D\cdot Q$ där $Q$ är en verkningsfaktor och för $\alpha$-strålning är $Q=20$. Vi får nu att $\begin{align*}
D=& \dfrac{H}{Q}=\dfrac{3{,}5\cdot 10^{-3}}{20}= 1{,}75\cdot 10^{-4}\textrm{ Sv}&&
\end{align*}$
men $D=\dfrac{E}{m}$ så vi får energin $\begin{align*}
\dfrac{E}{m}=& 1{,}75\cdot 10^{-4} \quad \Longrightarrow \quad E=85\cdot 1{,}75\cdot 10^{-4}=15 \textrm{ mJ} &&
\end{align*}$ |
|||||||||
| kf-053 | Radioaktiv kryptongas (krypton-81*) används vid lungundersökningar. Kryptongasen sänder ut gammastrålning. Halveringstiden är 13 s. En patient inandas luft som innehåller $6{,}00\cdot 10^{9}$ radioaktiva kryptonatomer. Patienten håller andan i 20 s.
Gammastrålningen från den luft som nu finns i lungorna, ger en bild av lungorna.
|
||||||||
|
|||||||||
|
|||||||||
| kf-054 | Figuren nedan visar söndefallsschemat för kärnan $\ce{^{28}Al}$.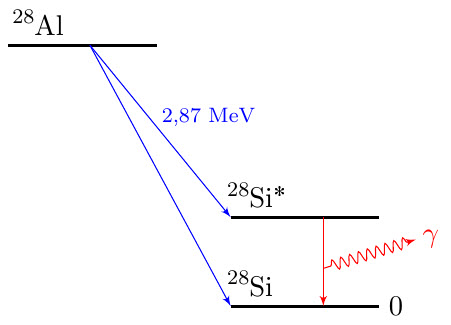
|
||||||||
|
|||||||||
|
|||||||||
| kf-055 | Radium sönderfaller till Radon via $\alpha$-sönderfall enligt $\textbf{(1/2/0)}$ $\begin{equation*}
\ce{^{226}_{88}Ra} \ce{ -> } \ce{^{222}_{86}Rn} + \ce{^{4}_{2}He}
\end{equation*}$
Beräkna massdefekten $\Delta m$ och den frigjorda energin för sönderfallet. Vilken hastighet skulle alfapartikeln få om både Radium- och Radonkärnorna kan antas vara i vila? |
||||||||
|
|||||||||
Massdefekten beräknas enkelt som skillnaden mellan nuklidmassorna före och efter. $\begin{align*}
\Delta m&= m\left(\ce{^{226}_{88}Ra}\right) - m\left(\ce{^{222}_{86}Rn} \right) - m\left(\ce{^{4}_{2}He}\right) &&\\[5pt]
&= 226{,}0254085 - 222{,}0175763 - 4{,}0026032541 = 0{,}0052289459 \textrm{ u}&&
\end{align*}$
Uttryckt i energi blir detta $\begin{align*}
E&= 0{,}0052289459 \cdot 931{,}49 = 4{,}870710816 \textrm{ MeV}&&\\[5pt]
&= 4{,}870710816 \cdot 10^6 \cdot 1{,}602 \cdot 10^{-19} = 7{,}80287873 \cdot 10^{-13} \textrm{ J}&&
\end{align*}$
Om $\alpha$-partikeln får hela denna energi som rörelseenergi kan hastigheten beräknas enligt $\begin{align*}
E&=\dfrac{mv^2}{2} \quad \Longrightarrow \quad v=\sqrt{\dfrac{2E}{m}}&&
\end{align*}$
massan för $\alpha$-partikeln är $\begin{align*}
m_{\alpha}&=4{,}0026032541-2\cdot 0{,}00045858 = 4{,}001506094 \textrm{ u}&&\\[5pt]
&=4{,}001506094 \cdot 1{,}660539 \cdot 10^{-27}=6{,}64465693 \cdot 10^{-27}\textrm{ kg}&&
\end{align*}$
Vi får då hastigheten till $\begin{align*}
v&=\sqrt{\dfrac{2E}{m}}=\sqrt{ \dfrac{2\cdot7{,}80287873 \cdot 10^{-13}}{6{,}64465693 \cdot 10^{-27}}} =15\,325\,200 \text{ m/s} = 0{,}05 \text{ c}&&
\end{align*}$
|
|||||||||
| kf-056 | Nickelkärnan $\ce{^{66}_{28}Ni}$ sönderfaller till koppar via ett $\beta^-$-sönderfall. Teckna reaktionsformeln för$\textbf{(1/2/0)}$ sönderfallet och beräkna massdefekten $\Delta m$ och den frigjorda energin för sönderfallet. Vilken hastighet skulle betapartikeln få om både nickel- och kopparkärnorna kan antas vara i vila? Nuklidmassorna för nickel och koppar är \begin{align*}
m\left(\ce{^{66}_{28}Ni}\right)&=65{,}929 139 \text{u}\\
m\left(\ce{^{66}_{28}Cu}\right)&=65{,}928 869 \text{u}
\end{align*} |
||||||||
|
|||||||||
Reaktionsformeln för sönderfallet blir $\begin{equation*}
\ce{^{66}_{28}Ni} \ce{ -> } \ce{^{66}_{29}Cu} + \ce{^{0}_{-1}e} + \bar{\nu_e}
\end{equation*}$
Eftersom det är ett $\beta^-$ sönderfall beräknas massdefekten enkelt som skillnaden mellan nuklidmassorna för modern minus dottern enligt. $\begin{align*}
\Delta m&= m\left(\ce{^{66}_{28}Ni}\right) - m\left(\ce{^{66}_{29}Cu}\right) &&\\[5pt]
&= 65{,}929 139 - 65{,}928 869 = 0{,}00027 \textrm{ u}&&
\end{align*}$
Uttryckt i energi blir detta $\begin{align*}
E&= 0{,}00027 \cdot 931{,}49 = 0{,}2515023 \textrm{ MeV}&&\\[5pt]
&= 0{,}2515023 \cdot 10^6 \cdot 1{,}602 \cdot 10^{-19} = 4{,}02906685 \cdot 10^{-14} \textrm{ J}&&
\end{align*}$
Om $\beta$-partikeln får hela denna energi som rörelseenergi $E_k$ kan hastigheten beräknas enligt $\begin{align*}
E_k&=\dfrac{mv^2}{2} \quad \Longrightarrow \quad v=\sqrt{\dfrac{2E_k}{m}}&&
\end{align*}$
$\beta$-partikeln är en elektron, så den massan hämtar vi direkt från formelsamlingen Vi får då hastigheten till $\begin{align*}
v&=\sqrt{\dfrac{2E_k}{m}}=\sqrt{ \dfrac{2\cdot 4{,}02906685 \cdot 10^{-14}}{9{,}1 \cdot 10^{-31}}} =297\,575\,066 \text{ m/s} = 0{,}9926 \text{c}&&
\end{align*}$
Hastigheten vi kommit fram till är mycket nära ljushastigheten $c=299\,792\,458$ m/s. Eftersom vår räkning är gjord med klassisk fysik, utan hänsyn till relativistiska effekter och hastigheten är mer än typ 10% av c, måste räkningen göras om med relativistiska metoder. Detta ingår egentligen inte i kursen, men för den intresserade läsaren gör jag den ändå. Den relativistiska rörelseenergin är lika med totala energin minus viloenergin och hanteras av uttrycket $\begin{align*}
E_k&=E_{\text{tot}}-E_0=\dfrac{mc^2}{\sqrt{1-\dfrac{v^2}{c^2}}}-mc^2=\gamma mc^2 - mc^2=mc^2(\gamma -1)&&
\end{align*}$
Här skulle vi kunna lösa ut hastigheten $v$ direkt genom att kvadrera och sedan lite algebra, men låt oss ta den lilla omvägen via $\gamma$-faktorn. $\gamma$-faktorn beräknas enligt $\begin{align*}
\gamma&=\dfrac{E_k}{mc^2}+1=\dfrac{4{,}02906685 \cdot 10^{-14}}{9{,}1 \cdot 10^{-31}\cdot 299\,792\,458^2}+1=1{,}492630929&&
\end{align*}$
Nu kan den korrekta relativistiska hastigheten beräknas enligt $\begin{align*}
\gamma&=\dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}&& \\[5pt]
1-\dfrac{v^2}{c^2}&=\dfrac{1}{\gamma^2} && \\[5pt]
v&=\sqrt{\left(1-\dfrac{1}{\gamma^2}\right)\cdot c^2}&& \\[5pt]
&=\sqrt{\left(1-\dfrac{1}{1{,}492630929^2}\right)\cdot 299\,792\,458^2}&& \\[5pt]
&=222\,565\,628 \text{ m/s}\approx0{,}74\text{c} &&
\end{align*}$
|
|||||||||
| kf-057 | När radioaktiva ämnen som återfinns i marken och i viss betong sönderfaller kan den radioaktiva radongasen Rn-222 bildas. Denna gas sönderfaller i sin tur genom alfasönderfall och bildar radondöttrar som lätt fastnar på damm som vi sedan andas in i våra lungor. Själva radongasen är inte direkt farlig för människan, men de radioaktiva radondöttrarna kan öka risken för lungcancer.
I Sverige har Boverket fastställt att radonaktiviteten i nya byggnader inte får överstiga 200 Bq/m$^3$ luft.
|
||||||||
|
|||||||||
|
|||||||||
| kf-058 | Beräkna massdefekten $\Delta m$ och bindningsenergin $E$ för en deuteriumkärna$\textbf{(1/1/0)}$ (kallas också för tungt väte) $\ce{^{2}_{1}H}$, skrivs även som $\ce{^{2}_{1}D}$. |
||||||||
|
|||||||||
Massdefekten $\Delta m$ för en deuteriumkärna $\ce{^{2}_{1}D}$ beräknas som skillnaden mellan summan av de fria partiklarnas massa och det bundna tillståndets massa. Observera också att kärnmassan för $\ce{^{2}_{1}D}$ är nuklidmassan ur tabellen minus den ensamma elektronens massa! $\begin{align*}
\Delta m&=\Big( m(p)+m(n)\Big)- \Big(m\left( \ce{^{2}_{1}D}\right)-m(e^-)\Big)&&\\[5pt]
&=1{,}007276+1{,}0086649158 - 2{,}01410177881+0{,}00054858 &&\\[5pt]
&=0{,}002387717 \text{ u}&&
\end{align*}$
Detta motsvarar bindningsenergin. $\begin{align*}
E&=\Delta m\cdot 931{,}49=0{,}002387717 \cdot 931{,}49=2{,}2241 \text{ MeV}&&
\end{align*}$
|
|||||||||
| kf-059 | Magnesium sönderfaller till Natrium via ett $\beta^+$-sönderfall enligt$\textbf{(1/2/0)}$ \begin{equation*}
\ce{^{23}_{12}Mg} \ce{ -> } \ce{^{23}_{11}Na} + \ce{^{0}_{1}e} + \nu_e
\end{equation*}
Beräkna massdefekten $\Delta m$ och den frigjorda energin för sönderfallet. Vilken hastighet skulle betapartikeln få om både Magnesium- och Natriumkärnorna kan antas vara i vila? |
||||||||
|
|||||||||
Eftersom det är ett $\beta^+$ sönderfall beräknas massdefekten enkelt som skillnaden mellan nuklidmassorna för modern minus dottern minus 2 elektronmassor enligt. $\begin{align*}
\Delta m&= m\left(\ce{^{23}_{12}Mg}\right) - m\left(\ce{^{23}_{11}Na}\right) - 2m\left(\ce{^{0}_{-1}e}\right) &&\\[5pt]
&= 22{,}9941239 - 22{,}989769282 -2\cdot 0{,}00054858= 0{,}003257458 \textrm{ u}&&
\end{align*}$
Uttryckt i energi blir detta $\begin{align*}
E&= 0{,}003257458 \cdot 931{,}49 = 3{,}034289552 \textrm{ MeV}&&\\[5pt]
&= 3{,}034289552 \cdot 10^6 \cdot 1{,}602 \cdot 10^{-19} = 4{,}86093186 \cdot 10^{-13} \textrm{ J}&&
\end{align*}$
Om $\beta$-partikeln får hela denna energi som rörelseenergi $E_k$ kan hastigheten beräknas enligt $\begin{align*}
E_k&=\dfrac{mv^2}{2} \quad \Longrightarrow \quad v=\sqrt{\dfrac{2E_k}{m}}&&
\end{align*}$
$\beta$-partikeln är en positron (exakt samma massa som elektronen), så den massan hämtar vi direkt från formelsamlingen Vi får då hastigheten till $\begin{align*}
v&=\sqrt{\dfrac{2E_k}{m}}=\sqrt{ \dfrac{2\cdot 4{,}86093186 \cdot 10^{-13}}{9{,}1 \cdot 10^{-31}}} =1\,033\,603\,731 \text{ m/s} = 3{,}447730934 \text{c}&&
\end{align*}$
Detta är såklart en helt orimlig hastighet som vi har kommit fram till, nästan 3,5 gånger ljusets hastighet (ljushastigheten $c=299\,792\,458$ m/s). Anledningen är att vår räkning är gjord med klassisk fysik, utan hänsyn till relativistiska effekter. En tumregel vid dessa räkningar är att klassisk räkning funkar helt ok ända upp till ungefär 10% av c, är hastigheten större behöver vi göra om räkningen med de relativistiska ekvationerna. Detta ingår egentligen inte i kursen, men för den intresserade läsaren gör jag den ändå. Den relativistiska rörelseenergin är lika med totala energin minus viloenergin och hanteras av uttrycket $\begin{align*}
E_k&=E_{\text{tot}}-E_0=\dfrac{mc^2}{\sqrt{1-\dfrac{v^2}{c^2}}}-mc^2=\gamma mc^2 - mc^2=mc^2(\gamma -1)&&
\end{align*}$
Här skulle vi kunna lösa ut hastigheten $v$ direkt genom att kvadrera och sedan lite algebra, men låt oss ta den lilla omvägen via $\gamma$-faktorn. $\gamma$-faktorn beräknas enligt $\begin{align*}
\gamma&=\dfrac{E_k}{mc^2}+1=\dfrac{4{,}86093186 \cdot 10^{-13}}{9{,}1 \cdot 10^{-31}\cdot 299\,792\,458^2}+1=3{,}437913922&&
\end{align*}$
Nu kan den korrekta relativistiska hastigheten beräknas enligt $\begin{align*}
\gamma&=\dfrac{1}{\sqrt{1-\dfrac{v^2}{c^2}}}&& \\[5pt]
1-\dfrac{v^2}{c^2}&=\dfrac{1}{\gamma^2} && \\[5pt]
v&=\sqrt{\left(1-\dfrac{1}{\gamma^2}\right)\cdot c^2}&& \\[5pt]
&=\sqrt{\left(1-\dfrac{1}{3{,}437913922^2}\right)\cdot 299\,792\,458^2}&& \\[5pt]
&=286\,829\,836 \text{ m/s}\approx0{,}95676\text{c} &&
\end{align*}$
|
|||||||||
