1.1 Kombinatorik
Lådprincipen (sid 8-10)
Boken presenterar denna princip tämligen kortfattat. På engelska kallas principen för Pigeonhole principle! Wikipedia artikeln är bra och beskriver principen mer utförligt för den intresserade studenten!
Principen är hur som helst simpel:
Antag att du ska placera 5 (eller fler) föremål i 4 lådor. Då säger lådprincipen att minst en låda måste innehålla minst två föremål (tänk igenom denna formulering).
Mer allmänt, om du placerar $n+1$ (eller fler) föremål i $n$ lådor så måste minst en låda innehålla minst två föremål.
Ännu mer allmänt, om du placerar $n\cdot k+1$ (eller fler) föremål i $n$ lådor så måste minst en låda innehålla minst $k+1$ föremål.
Om inte så hade vi ju haft högst $n\cdot k$ föremål, vilket vi ju INTE hade. Principen är enkel, men det som kan vara knepigt är att bestämma vad som ska fungera som lådor och vad som ska fungera som föremål, för detta krävs det en del övning lite fantasi. Bokens uppgifter är inte speciellt utmanande, om vi hinner kan vi ta lite klurigare extraövningar.
Exempel 1: Om du väljer fem nummer från heltalen 1-8, då måste summan av två av dem bli nio.
Varje nummer kan koppp med ett specifikt annat för att summera till nio. Det finns totalt fyra sådana par: 1 - 8, 2 - 7, 3 - 6, och slutligen 4 - 5. Var och en av de fem numren tillhör en av de fyra paren. Enligt lådprincipen måste två av talen vara från samma par, vilka sålunda summerar till 9.
| Övningsuppgifter sidan 10 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1104 | 1105 | 1106 | 1107 | 1108 | 1109 | 1110 | 1111 | 1112 | 1113 |
| 1114 | 1115 | ||||||||
Multiplikations- och additionsprincipen (sid 11-14)
Exempel 2: Antag att en restaurang erbjuder $p$ st förrätter och $q$ stycken varmrätter. Om du vill välja en förrätt och en varmrätt kan detta göras på $p\cdot q$ olika sätt (multiplikationsprincipen). Om du vill välja en förrätt eller en varmrätt kan detta göras på $p+q$ olika sätt (additionsprincipen). Tänk efter så ni är med på detta. Lite slarvigt kan man säga att och ger multiplikation och eller ger addition.
Exempel 3: Hur många olika registrieringsskyltar kan det finnas i det Svenska systemet om man bortser från de förväxlingsbara I,Q,V,Å,Ä,Ö?
Bokstaverna kan väljas på 23 sätt. I,Q,V,Å,Ä,Ö går bort. Siffrorna kan väljas på 10 sätt. 0-9. Enligt multiplikationsprincipen finns $n = 23\cdot 23\cdot 23\cdot 10\cdot 10\cdot 10 = 12\,167\,000$
| Övningsuppgifter sidan 13 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1118 | 1119 | 1120 | 1121 | 1122 | 1123 | 1124 | 1125 | 1126 | 1127 |
| 1128 | 1129 | 1130 | 1131 | 1132 | |||||
Permutationer (sid 15-18)
En permutation är en "uppräkning" av en mängd element/objekt i en viss ordning. Att beräkna antalet permutationer av $k$ element ur en mängd med $n$ element/objekt bygger på multiplikationsprincipen. Första elementet kan väljas på $n$ sätt, andra på $n−1$ sätt osv. till näst sista som kan väljas på $n−k+2$ sätt och det sista på $n−k+1$ sätt (tänk efter varför det inte blir $n−k$). Därmed får vi antalet permutationen av $k$ bland $n$ som
$\begin{align} P(n,k)=n \cdot (n-1) \cdot \ldots \cdot (n-k+2) \cdot (n-k+1) = \dfrac{n!}{(n-k)!} \end{align}$
där
$\begin{align} n! = 1 \cdot 2 \cdot \ldots \cdot (n-1) \cdot n \end{align}$
som utläses "n fakultet" (n factorial) är en praktisk beteckning. Ett "klassiskt" problem är att räkna antalet olika sexbokstavsord som man kan bilda av bokstäverna i ordet ANKFOT. Tydligen handlar det om $P(6,6)=6!=720$ stycken. Förresten, kan du ange ett riktigt ord som kan bildas förutom ANKFOT självt?
| Övningsuppgifter sidan 18 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1136 | 1137 | 1138 | 1139 | 1140 | 1141 | 1142 | 1143 | 1144 | 1145 |
| 1146 | 1147 | 1148 | 1149 | ||||||
Kombinationer (sid 19-22)
I förra avsnittet räknade vi antalet sätt att ordna $k$ element/objekt bland $n$. En sådan ordning kallades en permutation. Nu ska vi räkna antalet sätt att från $n$ element plocka ut $k$ stycken utan ordning. Ett sådant utval kallas en kombination. Tekniken är att man först räknar antalet permutationer
$\begin{align} P(n,k)=\dfrac{n!}{(n-k)!}. \end{align}$
Sedan noterar man att det finns $k!$ olika permutationer som ger upphov till samma oordnade utval (t.ex. ger ABC, ACB, BAC, BCA, CAB, CBA) upphov till samma oordnade urval {A,B,C}. Alltså grupperar vi ihop dessa permutationer till samma kombination och får då antalet kombinationer av $k$ element/objekt bland $n$ som
$\begin{align} C(n,k)={n \choose k} = \dfrac{P(n,k)}{k!} = \dfrac{n!}{k!(n-k)!} \end{align}$
där ${n \choose k}$ utläses "$n$ över $k$". Inför framtiden kan man också notera att uttrycket ${n \choose k}$ dyker upp i samband med binomialsatsen och därför ibland kallas binomialkoefficient.
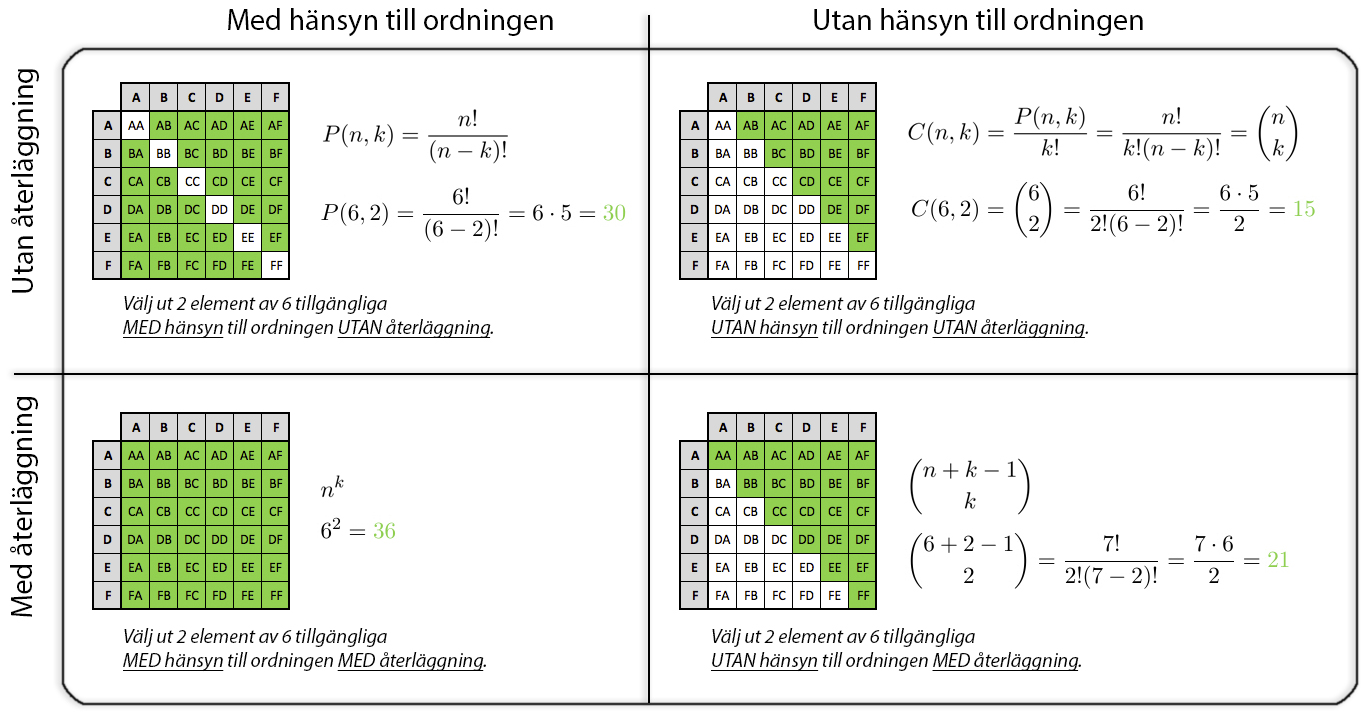
Jag har satt ihop en kort sammanfattning av de nya begreppen i figuren nedan och illustrerat det med exemplet att välja ut 2 element/objekt av 6 tillgängliga. De grönmarkerade rutorna i figurerna representerar då de aktuella urvalen.
| Övningsuppgifter sidan 22 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1153 | 1154 | 1155 | 1156 | 1157 | 1158 | 1159 | 1160 | 1161 | 1162 |
Kommer du ihåg sannolikhetslära? (sid 23-25)
Kombinatorik är såklart nära förknippat med sannolikhetslära. Vill man ta reda på sannolikheten beräknar man ju
$\begin{align} P=\dfrac{\textrm{antalet gynnsamma utfall}}{\textrm{totala antalet utfall}} \end{align}$
och talen i täljare och nämnare är ju kombinatoriska.
| Övningsuppgifter sidan 25 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1163 | 1164 | 1165 | 1166 | 1167 | 1168 | 1169 | 1170 | 1171 | 1172 |
Kombinatorik och sannolikhetslära (sid 26-27)
Finns inget att säga om detta mer än att det bygger på förra avsnittet.
| Övningsuppgifter sidan 27 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1174 | 1175 | 1176 | 1177 | 1178 | 1179 | 1180 | 1181 | 1182 | |
Binomialsatsen (sid 30-34)
Hur man utvecklar (multiplcerar ihop) $(x+y)^2$ är säkert bekant; nämligen enligt kvadreringsregeln
$\begin{equation} (x+y)^2=x^2+2xy+y^2 \end{equation}$
Binomialsatsen är i princip en formel för att utveckla $(x+y)^n$ för ett godtyckligt positivt heltal n. T.ex. kan man få en kuberingsregel
$\begin{align} (x+y)^3= (x+y)(x+y)(x+y)={3 \choose 0}x^3+{3 \choose 1}x^2y+{3 \choose 2} xy^2 + {3 \choose 3} y^3. \end{align}$
Man inser att koefficienten framför t.ex. $xy^2$ blir ${3 \choose 2}$ genom att tänka efter på hur många sätt man kan plocka ut två y (och därmed ett x) ur de tre parenteserna. Koefficienten ${n \choose k}$ kallas binomialkoefficient. Ett smidigt sätt att plocka fram binomialkoefficienterna är rekursivt via Pascals triangel. För att förstå att detta fungerar måste tänka igenom likheten
$\begin{align} {n \choose k} = {n-1 \choose k} + {n-1 \choose k-1} \end{align}$
vilket boken hjälper till med på sida 31-32. Det kombinatoriska argumentet på sida 31 är att föredra framför det algebraiska på sida 32.
| Övningsuppgifter sidan 34 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1186 | 1187 | 1188 | 1189 | 1190 | 1191 | 1192 | 1193 | 1194 | 1195 |
| 1196 | 1197 | ||||||||
1.2 Mängdlära
Mängder - Grundbegrepp (sid 35-38)
Här handlar det mest om att lära sig en del syntax (hur man skriver). Ganska tråkigt (men nödvändigt) att lära sig. Som kuriosa kan nämnas att vad som egentligen är en mängd och hur en sådan får defineras är mycket mer intrikat än boken medger, se t.ex. Barber paradox. Lös samtliga uppgifter utom 1203c. c-uppgifterna kan hoppas om man inte har höga betygsambitioner. I 1213 är n=11 det korrekta svaret!
| Övningsuppgifter sidan 38 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1204 | 1205 | 1206 | 1207 | 1208 | 1209 | 1210 | 1211 | 1212 | 1213 |
| 1214 | |||||||||
Mängdoperationer (sid 39-40)
Här inför man en sorts "räknesätt" på mängder, nämligen union, snitt, differens och komplement. Man noterar att för att komplementet ska ha mening måste grundmängden vara klar, för de övriga är det inte nödvändigt.
| Övningsuppgifter sidan 40 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1216 | 1217 | 1218 | 1219 | 1220 | 1221 | 1222 | 1223 | 1224 | |
Venndiagram (41-44)
Eftersom mängder kan ses som påsar med element i kan man tänka sig att representera dem grafiskt som "plana påsar". Man ritar helt enkelt en mängd som en cirkel (eller annan sluten kurva) och tänker sig att elementen ligger inuti cirkel. Ett finare namn för dessa cirklar är Venndiagram (efter John Venn). Ritar man lämpligt kan man illustrera snitt, unioner, komplement etc.
| Övningsuppgifter sidan 44 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1226 | 1227 | 1228 | 1229 | 1230 | 1231 | 1232 | 1233 | ||
1.3 Grafteori
Inledning (46-49)
Ordet graf har två olika betydelser inom matematik. Det som ni är vana vid är en "grafisk bild" kopplad till en funktion, t.ex. grafen till $f(x)=x^2$. Här är det fråga om något helt annat, en graf är något som byggs upp av Hörn (eller noder) sammankopplade med Kanter. Man kan se en graf som ett sorts nätverk eller karta. Det klasssika problemet som anses ha givit upphov till grafteorin är problemet med Königsbergs broar som beskrivs på sida 46. Teorigenomgången i boken är långt ifrån fullständig, vilket naturligtvis inte heller är ett mål, men jag tänkte komlettera den lite grand här.
| Begrepp | ||
|---|---|---|
| Hörn/Nod | Ett Hörn eller Nod kan ha gostyckligt många kanter som ansluter, eller ingen alls. | 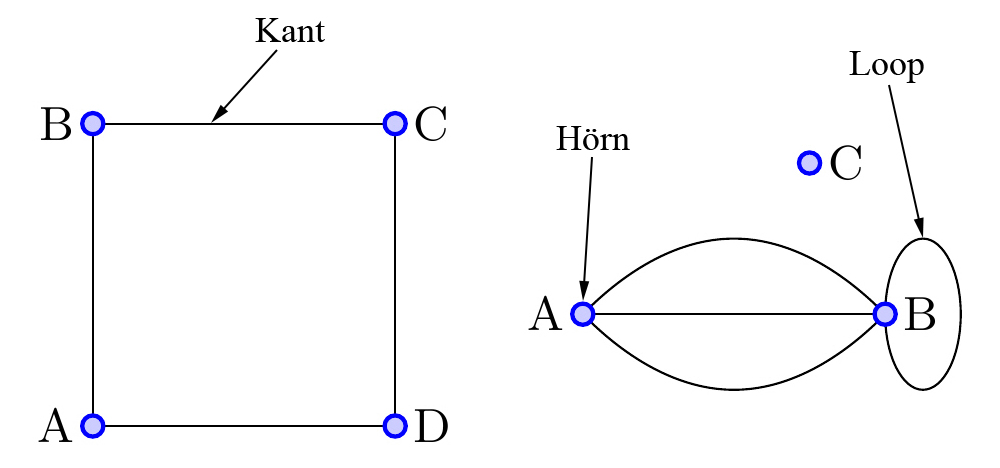 |
| Kant | En Kant är en förbindelse mellan två hörn. | |
| Loop/Ögla | Kant som börjar och slutar i samma hörn. | |
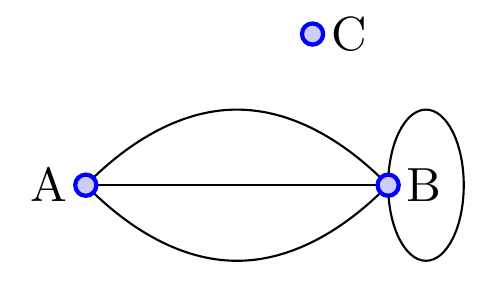
| Grad | Hörn har gradtal, vilket indikerar antalet kanter som ansluter till hörnet. deg(A)=3 |
 |
| Vandring | Förflyttning i en graf från hörn till hörn längs en eller flera kanter. | 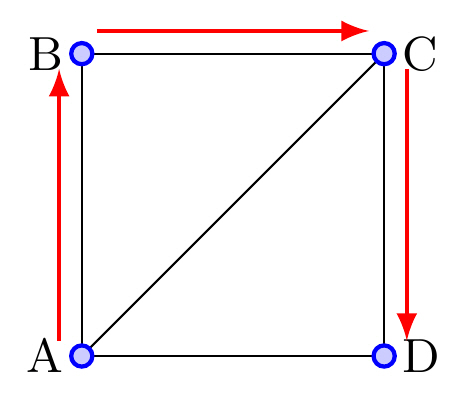 |
| Väg | Vandring i en graf som inte passerar någon kant mer än en gång. OBS! Hörn får passeras mer än en gång. |
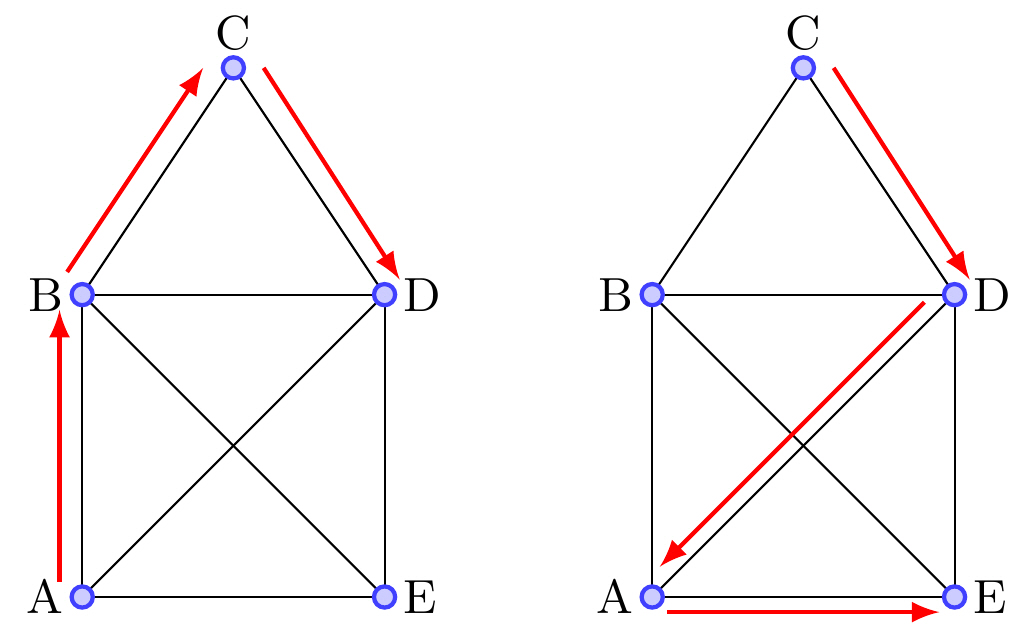 |
| Eulerväg | Väg som passerar varje kant exakt en gång. OBS! Hörn får passeras mer än en gång. Kan ha maximalt 2 hörn med udda gradtal |
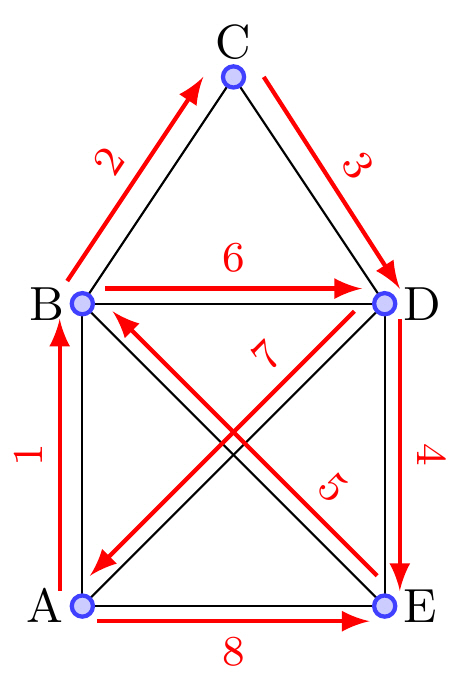 |
| Krets | Sluten väg, dvs. börjar och slutar i samma hörn. OBS! Hörn får passeras mer än en gång. |
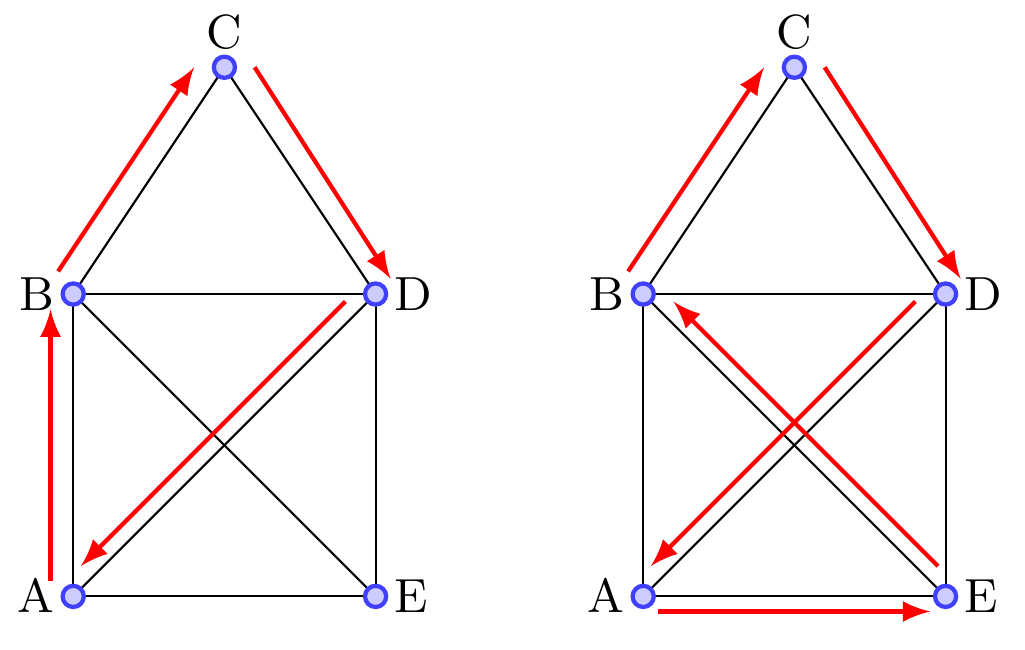 |
| Eulerkrets | Sluten Eulerväg Alla hörn måste vara av jämnt gradtal OBS! Hörn får passeras mer än en gång. |
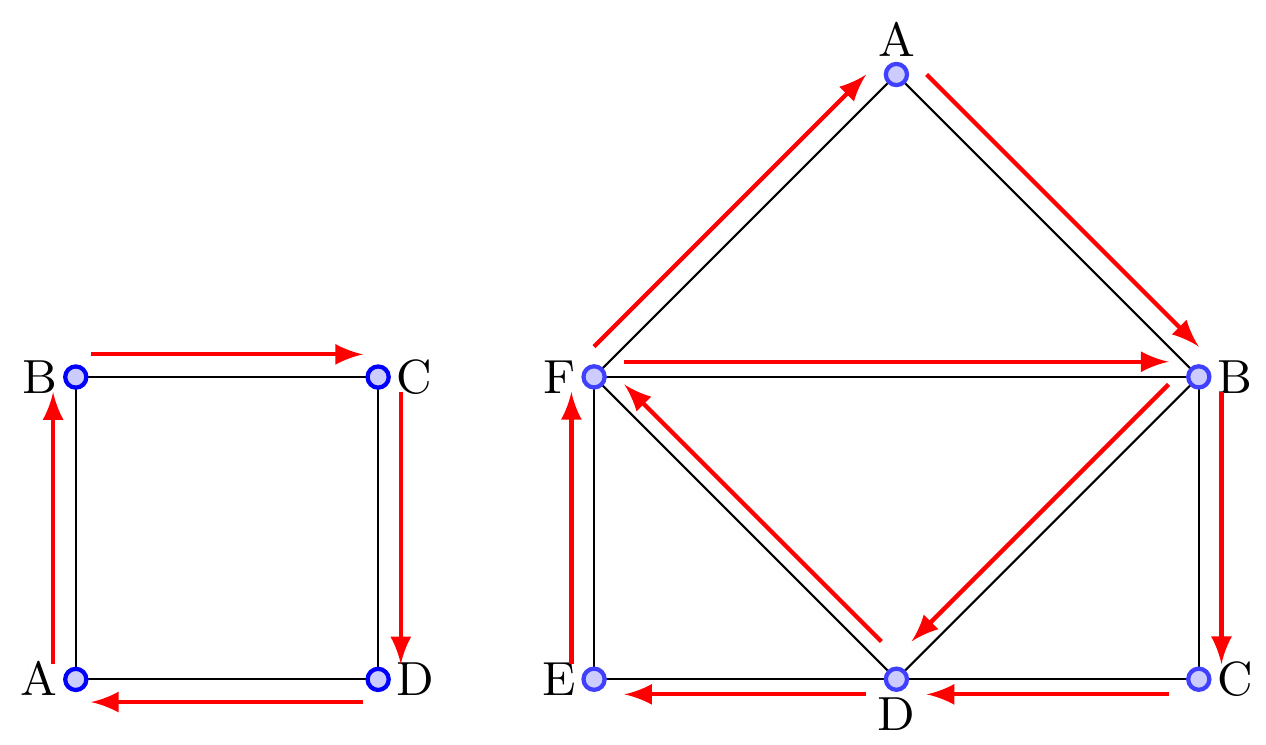 |
| Stig | Passerar inte samma kant eller hörn mer än en gång. | 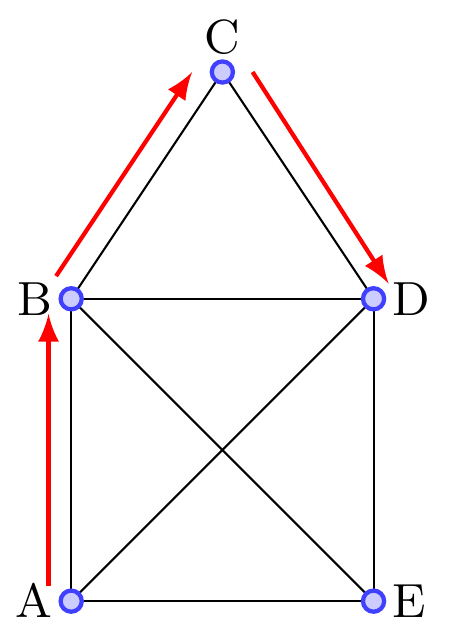 |
| Hamiltonstig | Passerar varje hörn exakt en gång. | 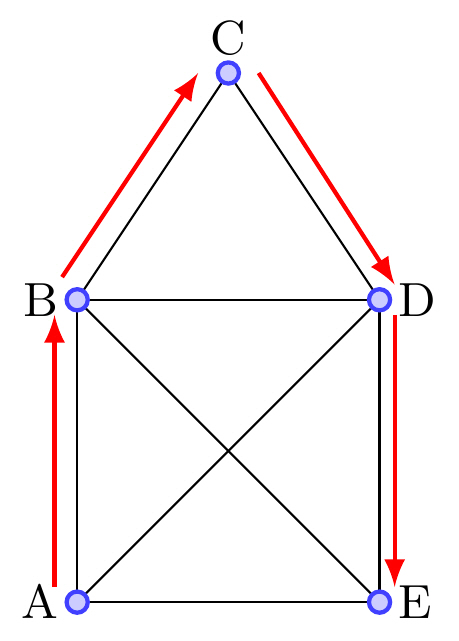 |
| Cykel | Sluten stig | 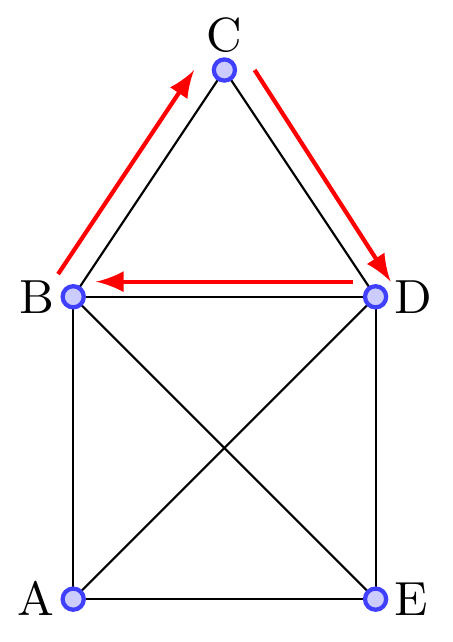 |
| Hamiltoncykel | Sluten Hamiltonstig | 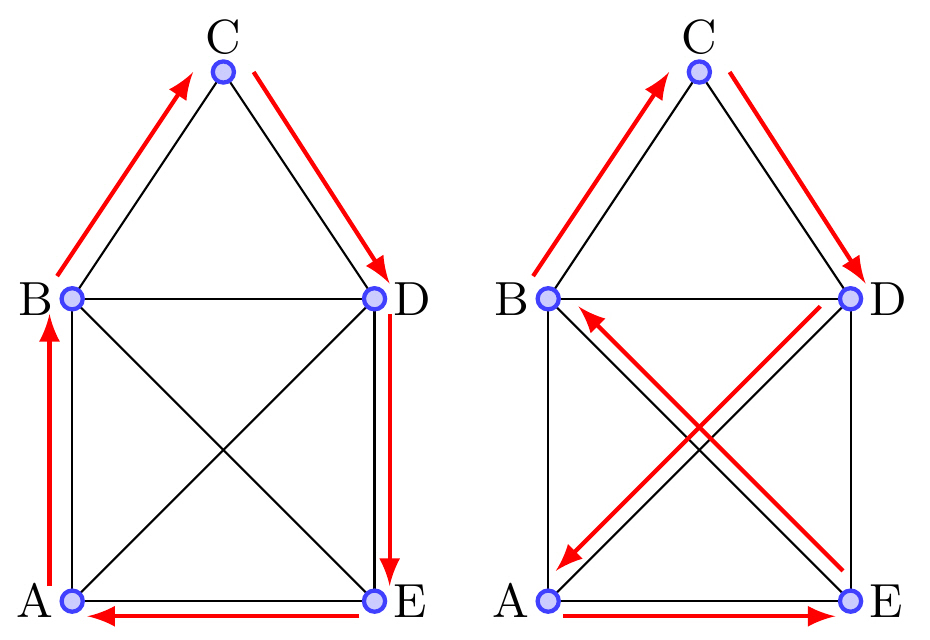 |
| Övningsuppgifter sidan 48 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1303 | 1304 | 1305 | 1306 | ||||||
Några klassiska problem (50-53)
Här handlar det om Hamiltoncykler, där det är fråga om att "åka" runt i en graf så att alla noder passeras en gång innan man är tillbaka där man startade. I 1312 ska man försöka finna Hamiltoncykler. Att visa att sådan finns är enkelt, rita den, men att visa att sådan inte finns kräver ett bättre argument än "jag kom inte på någon". I handelsresandes problem vill man, i en graf med viktade kanter, finna vägen med minsta kantsumma. För detta finns ingen riktigt bra algoritm (i alla fall har man inte kommit på någon) utan man nöjer sig med en s.k. girig algoritm där man varje gång väljer den bästa kanten. Konstruera gärna en graf där denna algoritm inte leder till optimal cykel.
| Övningsuppgifter sidan 52 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1308 | 1309 | 1310 | 1311 | 1312 | 1313 | ||||
Träd (sid 54-55)
Detta är ett ganska marginellt avsnitt. Ni behöver känna till vad ett träd är och Kruskals algoritm, som man kan använda för att koppla ihop noder "på billigaste sätt". Varför algoritmen fungerar ingår inte i kursen.
| Övningsuppgifter sidan 56 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1315 | 1316 | 1317 | 1318 | 1319 | |||||