1.1 Kraftmoment
Moment är en storhet som uppstår när en kraft verkar på en viss punkt.
Momentet = Kraft $\cdot$ hävarm.
$M=F\cdot l$
1.1.1 Tyngdpunkt (sid 12-16)
Även i detta avsnitt är Newtons Gravitationslag grunden för alla beräkningar.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
1.2 Cirkulär centralrörelse
1.2.1 Cirkulär centralrörelse (sid 19-24)
Jämför två scenarier med acceleration, rätlinjig och cirkulär.
 |
 |
|
Tänk dig till exempel att du är en passagerare i en bil vid ett trafikljus. Det blir grönt och föraren accelererar från stillastående. Bilen börjar att accelerera framåt, men i förhållande till sätet som du sitter på trycks din kropp bakåt mot ryggstödet. Känslan av att tryckas bakåt är bara en konsekvens av tröghetslagen, din kropp vill motstå accelerationen och stanna kvar i sitt tillstånd av vila. Bilen accelererar under kroppen och lämnar dig med den falska känslan av att ha skjutits bakåt. Tröghetslagen - "föremål i vila tenderar att stanna vid vila". |
Antag nu att du som passagerare i en bil gör en skarp sväng till vänster vid konstant hastighet. För enkelhetens skull antar vi också att bilen färdas i en cirkulär bana. Friktionskraften som verkar på hjulen på bilen orsakar en kraft på bilen och en efterföljande acceleration. Kraften och accelerationen är båda riktade mot mitten av cirkeln kring vilken bilen svänger. Din kropp är dock i rörelse och tenderar att stanna i rörelse. Det är trögheten i kroppen - tendensen att motstå acceleration - som får den att fortsätta sin rörelse framåt. Medan bilen accelererar inåt, fortsätter du i en rak linje. Om du sitter på passagerarsidan av bilen upplevs detta som om du tryckt utåt mot passagerardörren. Detta fenomen kan få dig att tro att du accelereras utåt bort från mitten av cirkeln. I verkligheten fortsätter du i din linjära tröghets tangent till bancirkeln. Känslan av en utåtriktad kraft och en utåtriktad acceleration är en falsk känsla. Det finns inget fysiskt föremål som kan skjuta dig utåt. Du bara upplever tendensen av din kropp vill fortsätta i sin linjära väg trots att bilen färdas i en cirkulära bana då den svänger. Du har kvar den falska känslan av att knuffas i en riktning som är motsatt din acceleration |
Sammanfattningsvis:
När du sitter i en bil som accelererar linjärt, alltså till exempel på en motovägspåfart. Då upplever du att din kropp trycks bakåt mot ryggstödet, men bilen accelererar framåt i färdriktningen. Du pressas alltså i en riktning motsatt accelerationsriktningen.
I fallet med färd genom cirkulär kurva med konstant fart upplever du att du pressas mot dörren utåt från cirkelcentrum, det är alltså rimligt att anta att accelerationen i detta fall också är motsatt riktad, dvs. innåt centrum!
| Övningsuppgifter sidan 25 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 |
| 122 | |||||||||
1.3 Gravitation och Keplers lagar
1.3.1 Keplers lagar (sid 28-31)
mer kommer...
| Övningsuppgifter sidan 32 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 123 | 124 | 125 | 126 | 127 | 128 | 129 | |||
1.4 Kaströrelse
Påminner om rörelseformlerna för konstant acceleration utmed en rät linje från Fysik 1
$v=v_0+at$, (Hastigheten $v$ vid tiden $t$.)
$x=v_0t+\dfrac{at^2}{2}$, (Läget $x$ vid tiden $t$.)
1.4.1 Horisontellt kast (sid 35-37)
I ett vågrätt kast är utgångshastigheten $v_0$ vågrät. Vi sätter startpunkten som origo i ett koordinatsystem där x-axeln är vågrät och y-axeln är lodrät.
Hastighetsformlerna fås enligt.
$v_x=v_0$
$v_y=-gt$
Föremålet påverkas alltså enbart av accelerationen $g$ i y-led. Fritt fall med andra ord!
1.4.2 Snett kast (sid 38-40)
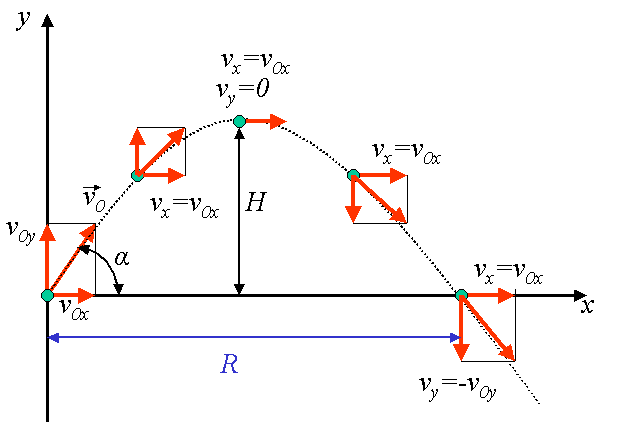
| x-led | y-led | |
|---|---|---|
| Acceleration | $a_x=0$ | $a_y=-g$ |
| Hastigehet | $v_x=v_{0x}=v_0\cdot \cos \alpha$ | $v_y=v_0\cdot \sin \alpha -gt$ |
| Läge | $x=v_{0x}\cdot t=v_0\cdot \cos \alpha \cdot t$ | $y=v_{0y}=v_0\cdot \sin \alpha \cdot t -\dfrac{gt^2}{2}$ |
Vad som är speciellt intressant att veta om kastparabeln är stigtiden $t_s$, stighöjden $H$ och kastvidden $R$! Dessa formler kan härledas relativt enkelt ur rörelelagarna ovan.
Stigtid: Sätt $v_y=0$
$\Rightarrow$ $t_s=\dfrac{v_0 \sin \alpha}{g}$
Stighöjd: $H$ fås ur läget i y-led vid tiden $t_s$.
$ \begin{aligned} H=y_{max}=y(t_s) & =v_0\cdot \sin \alpha \cdot t_s -\dfrac{gt_s^2}{2}&&\text{Tiden $t_s$} \\ & =v_0\cdot \sin \alpha \cdot \dfrac{v_0 \sin \alpha}{g} -\dfrac{g\left(\dfrac{v_0 \sin \alpha}{g} \right)^2}{2}&& \text{Stoppa in uttrycket för $t_s$}\\ & = \dfrac{v_0^2 \sin^2 \alpha}{g} -\dfrac{g\left(\dfrac{v_0^2 \sin^2 \alpha}{g^2} \right)}{2}&& \text{Algebra!}\\ & = \dfrac{v_0^2 \sin^2 \alpha}{g} -\dfrac{v_0^2 \sin^2 \alpha}{2g}&& \text{Algebra!}\\ & =\dfrac{v_0^2 \sin^2 \alpha}{2g}&& \text{Klart!} \end{aligned} $
Kastvidd: $R=x_{max}$ fås ur läget i x-led vid tiden $t=2t_s$.
$ \begin{aligned} R=x_{max}& =v_0\cdot \cos \alpha \cdot 2t_s &&\text{Tiden $t=2t_s$} \\ & =v_0\cdot \cos \alpha \cdot 2\left(\dfrac{v_0 \sin \alpha}{g}\right)&& \text{Stoppa in uttrycket för $t_s$}\\ & = \dfrac{v_0^2 \sin 2\alpha}{g}&& \text{Algebra, Klart!} \end{aligned} $
Även kastparabelns ekvation kan man härleda genom att lösa ut $t$ ur lägesformeln för $x$ och stoppa in detta i lägesformeln för $y$. Man får.
$y=\tan \alpha \cdot x - \dfrac{g}{2v_0^2 \cos^2\alpha} \cdot x^2$
Slutligen lite överkurs, om man också lägger till en utgångshöjd över (eller under) horisontalplanet får man följande uttryck för kastvidden.
$R=x_{max}=\dfrac{v_0 \cos \alpha}{g}\left(v_o \sin \alpha + \sqrt{v_0^2 \sin^2 \alpha + 2gh}\right)$
1.4.3 Kast med räknarens hjälp (sid 41-42)
mer kommer...
1.4.4 Kast med luftmotstånd (sid 43)
mer kommer...
| Övningsuppgifter sidan 44 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 130 | 131 | 132 | 133 | 134 | 135 | 136 | 137 | 138 | |