4.2 Vågrörelselära
Interferens i dubbelspalt (sid 223-224)
Här går vi igenom diffraktion och interferens
| Ljusmaxima i dubbelspalt |
|---|
| $d\sin \alpha_k=k\cdot \lambda$ med $k=1,2,3,...$ |
Interferens i gitter (sid 224-228)
Ett gitter är en yta med flera smala spalter på avståndet $d$ från varandra.
| Ljusmaxima i ett gitter |
|---|
| $d\sin \alpha_k=k\cdot \lambda$ med $k=1,2,3,...$ |
| Övningsuppgifter sidan 228 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 410 | 411 | 412 | 413 | 414 | 415 | 416 | 417 | 418 | 419 |
| 420 | |||||||||
Diffraktion i enkelspalt (sid 230)
Notera att ljusminima i en enkelspalt lyder samma relation som för ljusmaxima i ett gitter.
| Ljusminima i enkelspalt |
|---|
| $d\sin \alpha_k=k\cdot \lambda$ med $k=1,2,3,...$ |
Dopplereffekt (sid 231)
Precis som för ljudvågor kan även ljusvågos frekvens och våglängd upplevas olika beroende på den relativa hastigheten.
| Dopplereffekt |
|---|
| $\dfrac{\lambda}{\lambda_0}=\dfrac{f_0}{f}=\dfrac{\sqrt{1+\frac{v}{c}}}{\sqrt{1-\frac{v}{c}}}\approx 1+\dfrac{v}{c}$ |
Radiokommunikation (sid 232-233)
Kort om raiokommunikation
| Övningsuppgifter sidan 234 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 421 | 422 | 423 | 424 | 425 | 426 | 427 | |||
4.3 Temperaturstrålning
Svartkroppsstrålning (sid 235-239)
Föremål avger strålning i relation till dess temperatur.
| Emittans |
|---|
| $M=\dfrac{P}{A}$ |
| Plancks strålningslag |
|---|
| $\dfrac{dM}{d\lambda}=\dfrac{2\pi hc^2}{\lambda^5}\dfrac{1}{e^{\frac{hc}{\lambda kT}}-1}$ |
| Stefan-Boltzmanns lag |
|---|
| $M=\dfrac{2\pi^5 k^4}{15h^3c^2}\cdot T^4=\sigma T^4$ |
| Wiens förskjutningslag |
|---|
| $\lambda_{\text{max}}T=2{,}8978\cdot 10^{-3}$ m K (meter multiplicerat med Kelvin) |
| Övningsuppgifter sidan 240 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 428 | 429 | 430 | 431 | 432 | 433 | 434 | 435 | 436 | 437 |
4.4 Stråloptik
Reflektion (sid 241)
Några enkla men viktiga fenomen
| Reflektionslagen |
|---|
| $i=r$ |
Brytning (sid 242-244)
Några enkla men viktiga fenomen
| Brytningslagen |
|---|
| $\dfrac{\sin i}{\sin b}=\dfrac{n_2}{n_1}$ eller $n_1 \sin i =n_2\sin b$ |
| Övningsuppgifter sidan 245 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 438 | 439 | 440 | 441 | 442 | |||||
Interferens i tunna skikt (sid 246-250)
Intressant, men inte högprioriterat avsnitt.
| Övningsuppgifter sidan 251 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 443 | 444 | 445 | 446 | 447 | 448 | ||||
4.5 Ljus är en partikelström
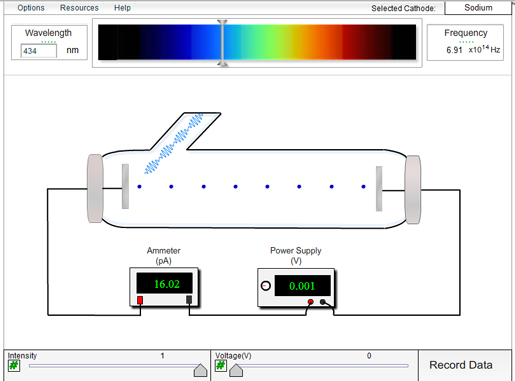
Fotoelektrisk effekt (sid 252-256)
Viktig fundamental upptäckt av Einstein, vilken också gav honom 1921 års nobelpris i fysik.
| Fotoelektrisk effekt |
|---|
| $E_k=hf-E_0$ |
En bra app från The King's Centre for Visualization in Science.
Fotonen kan aldrig vara i vila och saknar således vilomassa och vi säger definitionsmässigt därför att fotonen därmed är masslös. Den har däremot en energi, en frekvens och en rörelsemängd, men begrepp som massa, storlek och läge kan inte definieras på ett meningsfullt sätt.
Fotonen har energin
$E=hf$, där $h=6.626\cdot 10^{-34}$Js är Placks konstant.
Eftersom energi och massa är ekvivalenta (via Einstens berömda formel $E=mc^2$), så har fotonen i någon mening ändå en ekvivalent massa. För alla partiklar eller objekt som har en vilomassa $m_0$ skulle det krävas en oändlig mängd energi att accelerera den till ljusets hastighet. I klassisk mening finns ingen sådan hastighetsbegränsning, rörelseenergin $E_k$ växer enligt $E_k=\dfrac{mv^2}{2}$ (den svarta kurvan nedan).
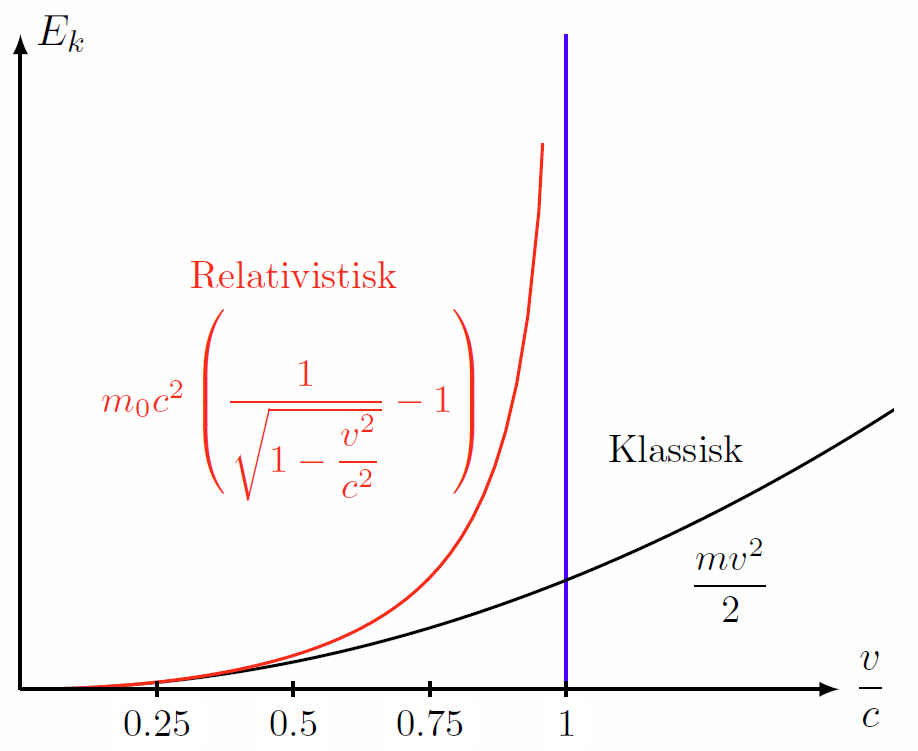
Den klassiska beskrivningen av rörelsemängd från fysik 1 kursen är att
$p=m\cdot v$
Fotonen saknar alltså vilomassa och den rör sig alltid med ljusets hastighet. Fotonens rörelsemängd $p$ blir
$p=\dfrac{E}{c}=\dfrac{hf}{c}=\dfrac{h}{\lambda}$
| Fotonens energi |
|---|
| $E_{\text{foton}}=hf$ |
| Fotonens rörelsemängd |
|---|
| $p_{\text{foton}}=\dfrac{h}{\lambda}$ |
| Övningsuppgifter sidan 257 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 449 | 450 | 451 | 452 | 453 | 454 | 455 | 456 | ||
Comptoneffekten (sid 258)
Kollisioner mellan fotoner och elektroner.
| Comptoneffekten |
|---|
| $\lambda_2-\lambda_1=\dfrac{h}{mc}(1-\cos \alpha$ |
Parbildning (sid 258)
Ytterligare ett fenomen som kan ske då ljus träffar materia.
Annihilation (sid 259)
Detta är omvändningen till parbildningsfenomenet.
Absorption av fotoner (sid 260-262)
Det finns i huvudsak tre olika fenomen där fotoner avger energi till elektroner.
| Övningsuppgifter sidan 263 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 457 | 458 | 459 | 460 | 461 | 462 | 463 | 464 | 465 | |
Röntgenstrålar (sid 264-267)
Elektroner kolliderar med metaller och så kallad bromsstrålning kan sändas ut.
| Bromsstrålningens kortaste våglängd |
|---|
| $\lambda_{\text{min}}=\dfrac{hc}{eU}$ |
| Övningsuppgifter sidan 268 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 466 | 467 | 468 | 469 | 470 | 471 | ||||
4.7 Atomens elektronstruktur
Väteatomen (sid 274)
Grundämnen "lyser" med olika färg.
| Vätets spektrum |
|---|
| $\dfrac{1}{\lambda}=R_H\left(\dfrac{1}{n_1^2}-\dfrac{1}{n_2^2}\right)$ |
Bohrs atommodell (sid 274-277)
Kvanthypotesen:
En atom kan bara sända ut eller ta emot energi i bestämda portioner eller kvanta.
$E=hf$
Energin ($E$) är lika med Plancks konstant ($h=6.626 \cdot 10^{-34}$) multiplicerat mer frekvensen $f$.
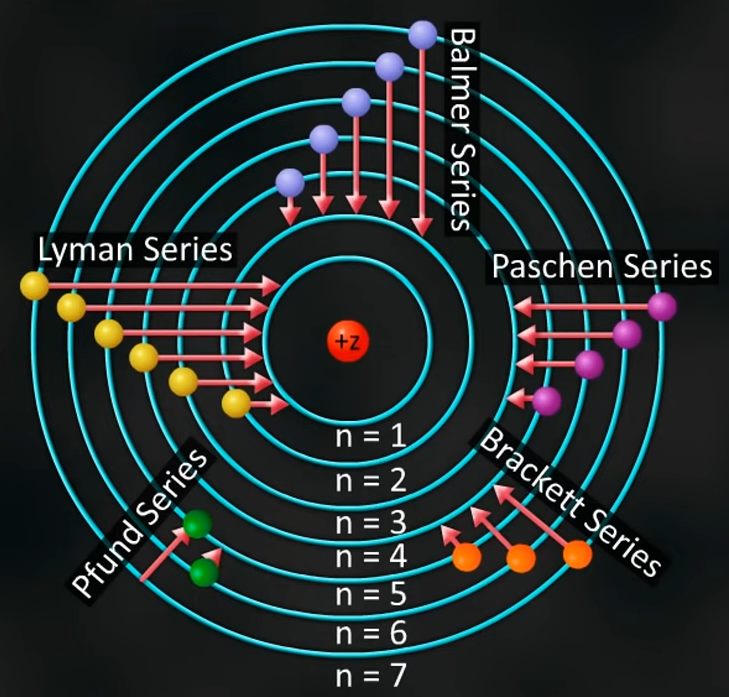
Bohrs modell av väteatomen kallas också skalmodellen, han föreställde sig en atom som bilden nedan.
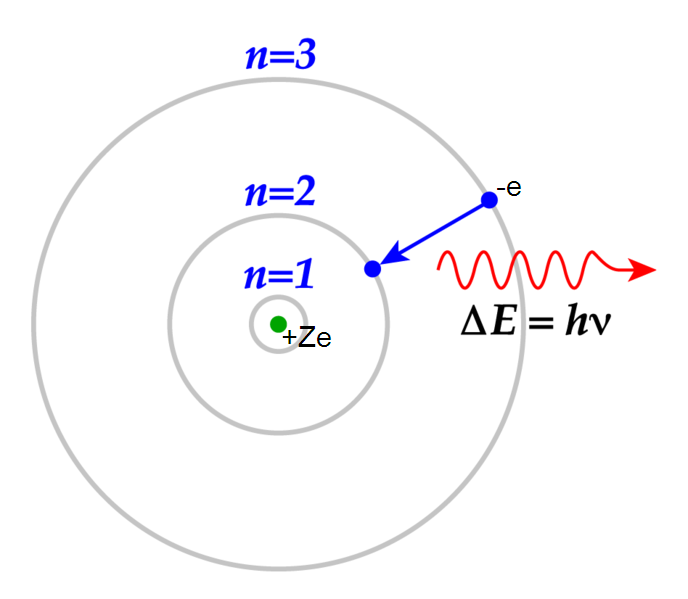
Kolla även in denna korta video som visar väteatomens spektrallinjer och hur de uppkommer.
Väteatomens elektron, och alla andra atomers elektroner också för den delen, kan exciteras. Detta innebär att de tillförs ett energikvanta (en foton) med tillräckligt stor energi för att "lyfta upp" elektronen ett eller flera energisteg. Elektronerna vill hela tiden befinna sig i sitt grundtillstånd, därför kommer de nästan omedelbart att hoppa tillbaka dit och då gör de sig av med den energi som de precis fått i form av av elektromagnetisk strålning. Beroende på hur stort tillbakahoppet är, blir strålningen som den skickar ut olika energirik. Ju mer energi strålningen innehåller, desto kortare våglängd blir det.
V
arje atom har sin unika uppsättning energinivåer. Nedan är vätets energinivå diagram i två olika skepnader. Negativa energinivåer därför att den joniserade väteatomen (d v s då elektronen avlägsnats) antas ha energin 0 eV.
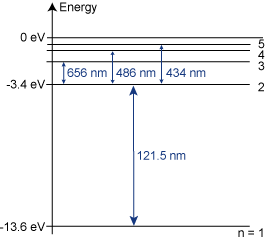
Hur kan man beräkna exempelvis våglängden på ljuset från $H_{\alpha}$ övergången? Alltså när vätets elektron faller ner från nivå 3 till nivå 2.
Genomgång av energienheten Elektronvolt eV
Se YouTubeklippet med denna beräkning.
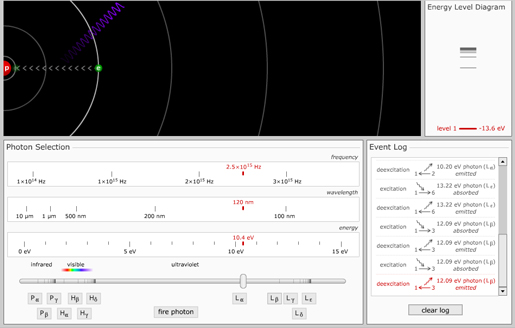
Här finns en app som simulerar väteatomens energinivåer. Genom att justera slidern kan ni bombardera elektronen med godtyckliga fotonenergier. I loggen ser ni vilka övergångar som genereras.
Försök exempelvis få fram den välkända övergången som generarar $H_{\alpha}$ linjen.
| Övningsuppgifter sidan 278 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 480 | 481 | 482 | 483 | 484 | 485 | 486 | 487 | ||
Atomspektrum (sid 279-282)
Kombinerar man Newtons Gravitationslag
Atom- och molekylidentifiering (sid 282-285)
Kombinerar man Newtons Gravitationslag
| Övningsuppgifter sidan 285 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 488 | 489 | 490 | 491 | 492 | |||||