3.1 Integraler och areor
Primitiva funktioner (sid 150-153)
Repetition från Ma3c. Läs igenom detta och öva upp handhavandet med de olika deriveringsreglerna.
Se till att ha koll på de generella deriveringsreglerna.
$D\left(k\cdot f(x)\right)=k\cdot f'(x)$
$D\left(f(x) \pm g(x)\right)=f'(x) \pm g'(x)$
| Övningsuppgifter sidan 153 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3104 | 3105 | 3106 | 3107 | 3108 | 3109 | 3110 | 3111 | 3112 | 3113 |
| 3114 | 3115 | ||||||||
Integralberäkningar (sid 154-158)
Beviset för derivatan av en produkt, den såkallade produktregeln kan se ut såhär. Lite annorlunda jämfört med bokens bevis.
Sats: Om både $f(x)$ och $g(x)$ är deriverbara gäller för produkten av dessa att $y=f(x)\cdot g(x)$ $\Longrightarrow$ $y'=f'(x) \cdot g(x) + f(x) \cdot g'(x)$.
Bevis:
$\small \begin{aligned} y'(x) & = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h)g(x+h) - f(x)g(x)}}{h} &&\text{Derivatans definition} \\ & = \mathop {\lim }\limits_{h \to 0} \frac{{f(x + h)g(x+h) -f(x)g(x+h) +f(x)g(x+h) - f(x)g(x)}}{h} && \text{Trix med $f(x)g(x+h)$}\\ & = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(x + h)g(x+h) -f(x)g(x+h)}}{h}} \right) + \mathop {\lim }\limits_{h \to 0}\left( {\frac{{f(x)g(x+h) - f(x)g(x)}}{{h}}} \right) && \text{Dela upp i bråk}\\ & = \mathop {\lim }\limits_{h \to 0} \left( {\frac{{f(x + h) -f(x)}}{h}} g(x+h) \right) + \mathop {\lim }\limits_{h \to 0}\left(f(x) {\frac{{g(x+h) - g(x)}}{{h}}} \right) && \text{Bryt ut $g(x+h)$ & $f(x)$}\\ & = f'(x) g(x) + f(x) g'(x) &&\text{Klart!} \end{aligned} $
| Övningsuppgifter sidan 157 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3118 | 3119 | 3120 | 3121 | 3122 | 3123 | 3124 | 3125 | 3126 | 3127 |
| 3128 | 3129 | 3130 | 3131 | 3132 | 3133 | 3134 | |||
Area under x-axeln (sid 159-162)
Om vi nu har en funktionen i form av en kvot av funktioner $y=\dfrac{f(x)}{g(x)}$. Hur skall vi derivera denna? Jo, då tar vi hjälp av kvotregeln.
$y'=\dfrac{f'(x)g(x)-f(x)g'(x)}{(g(x))^2}$
Men kvotregeln är egentligen överflödig. Det går alltid bra att använda produktregeln ï kombination med kedjeregeln enligt.
$\small y=f(x)(g(x))^{-1}$
$\small y'=f'(x)(g(x))^{-1} + f(x)\cdot (-1)(g(x))^{-2} \cdot g'(x)= \dfrac{f'(x)}{g(x)}-\dfrac{f(x)g'(x)}{(g(x))^2}=\dfrac{f'(x)g(x)-f(x)g'(x)}{(g(x))^2}$
Träna på dessa regler så att ni känner att ni behärskar dem.
| Övningsuppgifter sidan 161 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3137 | 3138 | 3139 | 3140 | 3141 | 3142 | 3143 | 3144 | 3145 | 3146 |
Arean mellan två kurvor (163-167)
Vi vet sedan tidigare att exponentialfunktionen med basen $e$ blir sin egen derivata, alltså om
$f(x)=e^x$
så blir derivatan också
$f'(x)=e^x$.
Men varför blir det så? Återigen kan vi få bättre förståelse för detta genom att utnyttja derivatans definition.
$\small
\begin{aligned}
f'(x) &=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}&&\text{Derivatans definition} \\
& = \lim_{h \to 0}\frac{ e^{(x+h)}- e^x}{h} && \text{Stoppa in funktionen}\\
& = e^x\cdot \lim_{h \to 0}\frac{ e^h-1}{h} && \text{Bryt ut $e^x$ och beräkna gränsvärdet!}\\
& =e^x \cdot \ln e = e^x &&\text{Klart!}
\end{aligned}
$
Här kan man börja ana att talet $e$ intar en särställning bland alla tal och då menar jag verkligen ALLA tal. För om vi hade haft en exponentialfunktion med någon annan bas, säg $a$ då hade ju det där gränsvärdet konvergerat mot ett tal $\neq$1 och vi hade fått en extra faktor framför derivatan och det är opraktiskt och absolut inte lika vackert!
Nu tar vi hjälp av GeoGebra igen och skall visualisera ovanstående, dvs. derivatan av den allmänna exponentialfunktionen
$f(x)=a^x$
Exponentialfunktion med basen $e$ har många andra intressanta egenskaper. Här illustreras en till.
Om vi nu går över till logaritmfunktionen istället kan vi först konstatera att den är inversen till exponentialfunktionen. Dvs. $e^x$ är invers till $\ln x$ och vice versa. Det innebär i vanliga ordalag att dessa funktioner tar ut varandra, som exempelvis om $f(x)=x^2$ och $g(x)=\sqrt{x}$. Då får man ju att $(\sqrt{x})^2 = x$ och på motsvarande sätt att $\sqrt{x^2} = x$. Åtminstone om $x \geq 0$ får väl tilläggas!
I praktiken är det två baser som oftast används för logaritmer, förutom basen 10, som då skrivs log$_{10}$, används även talet $e$ (2.71828...). Logaritmer med basen $e$ kallas naturliga logaritmer och skrivs $\ln$ i stället för log$_e$.
Vidare, en funktion och dess invers har en del intressanta egenskaper som vi kan utnyttja här. Det finns en matematisk sats som heter inversa funktionssatsen. Denna sats bevisar att om en funktions derivata existerar och är skild från noll på ett visst intervall så är också dess invers deriverbar på ett motsvarande intervall. Satsen ger oss också verktyg för att ta fram denna derivata med hjälp av kedjeregeln. Och det här är precis vad vi behöver nu när vi vill derivera $\ln x$. $\ln x$ är ju inversen till $e^x$ och $e^x$ vet vi att vi kan derivera och alltså bör också inversen $\ln x$ gå att derivera!
Så hur kan detta göras? Först kan ni kolla på denna GeoGebra konstruktion som indikerar hur derivatan bör se ut! Den visar på förhållandet mellan tangentens lutning och tillhörande x-värde!
Det teoretiska resonemanget illustrerar jag med några exempel.
Kalla våra motsats funktioner för $f$ och $g$ och använd kedjeregeln enligt följande.
Exempel 1: Om $f(x)=x^2$ och $g(x)=\sqrt{x}$ så ger kedjeregeln följande.
$\small
\begin{aligned}
f(g(x))&=\left(\sqrt{x}\right)^2=x &&\text{Kedjeregeln} \\
D\left(f(g(x))\right)&=f'(g(x))\cdot g'(x)=2\sqrt{x} \cdot g'(x)=D(x)=1 &&\text{Derivera båda sidor}\\
g'(x)&=\dfrac{1}{2\sqrt{x}} && \text{Klart!}\\
\end{aligned}
$
Exempel 2: Om $f(x)=e^x$ och $g(x)=\ln x$ så ger kedjeregeln följande.
$\small
\begin{aligned}
f(g(x))&=e^{\ln x}=x &&\text{Kedjeregeln} \\
D\left(f(g(x))\right)&=f'(g(x))\cdot g'(x)=e^{\ln x} \cdot g'(x)=D(x)=1 &&\text{Derivera båda sidor}\\
g'(x)&=\dfrac{1}{e^{\ln x}}=\dfrac{1}{x} && \text{Klart!}\\
\end{aligned}
$
Exempel 3: Om $f(x)=\sin x$ och $g(x)=\arcsin x$ så ger kedjeregeln följande.
$\small
\begin{aligned}
f(g(x))&=\sin(\arcsin x)=x &&\text{Kedjeregeln} \\
D\left(f(g(x))\right)&=f'(g(x))\cdot g'(x)=\cos(\arcsin x) \cdot g'(x)=D(x)=1 &&\text{Derivera båda sidor} \\
g'(x)&=\dfrac{1}{\cos(\arcsin x)}=\dfrac{1}{\sqrt{1-\sin^2(\arcsin x)}}=\dfrac{1}{\sqrt{1-x^2}} && \text{Klart!} \boxed{\cos x=\sqrt{1-\sin^2 x}}\\
\end{aligned}
$
Med hjälp av kedjeregeln och lite trix kan man även derivera funktionen $x^x$. Om ni läser lite mer matematik på universitet eller högskola så kommer ni få nya kraftfulla verktyg för att hantera bl.a. klurigare derivator. Vår kedjeregel har en motsvarighet inom flervariabelanalysen, om man exempelvis här bildar funktionen $g(y,z) = y^z$ av 2 variabler så kan man skriva $x^x = g(h(x),h(x))$, där $h(x) = x$. Man kan sedan använda kedjeregeln för funktioner av två variabler för att utföra derivationen. Men nu har vi inte tillgång till dessa verktyg ännu och blir därför hänvisade till envariabeltrix!
Exempel 4: Derivera $f(x)=x^x$.
$\small
\begin{aligned}
f(x)&=x^x=(e^{\ln x})^x=e^{x\ln x}&&\text{Omskrivning med log-lagarna} \\
D\left(e^{x\ln x}\right)&=e^{x\ln x}\cdot (\ln x +1)=x^x\cdot (\ln x +1) &&\text{Klart efter omskrivning.} \\
\end{aligned}
$
| Övningsuppgifter sidan 165 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 3149 | 3150 | 3151 | 3152 | 3153 | 3154 | 3155 | 3156 | 3157 | 3158 |
| 3159 | 3160 | 3161 | 3162 | 3163 | 3164 | ||||
Samband mellan förändringshastigheter (sid 113-115)
Kommer ni ihåg uppgiften på fysikprovet om stenen som kastades i en damm. I den övningen så var givet att radien växte med 30 cm per sekund. Man kan då fråga sig hur mycket växer arean av cirklen vid en viss radie! Detta är en typ av problem som återigen kan lösas med hjälp av kedjeregeln. Börja med att sätta upp ett uttryck för arean som funktion av radien.
$A(r)=\pi r^2$
Eftersom radien nu växer med tiden så måste vi i sin tur behandla radien som en funktion av tiden.
$r=r(t)$
Vår fråga i detta fall är ju hur arean växer med tiden, så funktionen för arean skall alltså deriveras med avseende på tiden och inte enbart med avseende på radien. Vi söker alltså derivatan till
$A\left(r(t)\right)=\pi r(t)^2$
$A'\left(r(t)\right)=A'\left(r(t)\right)\cdot r'(t)=2\pi r(t)\cdot r'(t)$
där $r'(t)$ enligt förutsättningarna är 30 cm/s. Boken använder noteringen
$\dfrac{dA}{dt}=\dfrac{dA}{dr}\cdot \dfrac{dr}{dt}$
där $r'(t)=\dfrac{dr}{dt}$ är den hastighet som radien växer med, dvs. 30 cm per sekund i vår uppgift! Så om vi nu vill veta hur mycket arean av cirkeln växer vid exempelvis $r=3$m. fås
$A'\left(r(t)\right)=2\pi\cdot 3\cdot 0.3=5.7$m$^2$/s.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
3.2 Tillämpningar av integraler
Integraler och storheter (sid 168-173)
Inget nytt här egentligen, i princip är detta redan gjort i Ma3c. Ni skall använda derivatan för att studera funktionsgrafer och bestämma max/min värde. Enda skillnaden är att ni nu förfogar över en något större verktygslåda och klarar därmed av att derivera fler funktioner. Glöm ej att att studera andraderivatans tecken för att avgöra max- eller minvärde. Alternativt genom att göra en teckenstudie. Det räcker inte att påstå att derivatan är noll.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Sannolikhetsfördelning (sid 174-181)
Definitionsmängd och värdemängd känner ni till sedan tidigare. Kontinuerlig betyder ungefär att funktionsgrafen hänger ihop där den är definierad. Deriverbar betyder ungefär att grafen inte har några hörn. Boken slarvar lite med dessa begrepp på några olika ställen. I exempel 1 är några av funktionerna inte definierade i $x=0$ och då är det heller ingen mening att prata om kontinuitet och deriverbarhet här.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Rotationsvolymer (sid 182-189)
Asymptoter är bra att utnyttja när man ska skissa utseendet hos en graf. Vad man gör är att man undersöker vad som händer med funktionen för stora värden på $x$. Titta exempelvis på grafen till $y=1/x$, den har två asymptoter, nämligen x-axeln som grafen närmar sig då $\left| {x} \right|$ är stort och y-axeln som grafen närmar sig då $\left| {x} \right|$ är litet. Tips är alltså att leta efter asymptoter i punkter där funktionen inte är definierade och "långt bort" längs x-axeln.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
3.3 Differentialekvationer
Begreppet differentialekvation (sid 128-133)
Definition:
En ekvation är ett algebraisk samband mellan tal, där det ingår ett okänt tal (ofta kallat $x$), som vanligtvis ska bestämmas. Exempel.
$3x-6=0$
En differentialekvation är ett algebraiskt samband mellan funktioner, där det ingår en okänd funktion och dess derivator. Exempel.
$3y'-6y=0$
Att lösa differentialekvationen betyder att bestämma funktionen y. I detta kapitel kommer ni inte att direkt lära er att lösa dessa ekvationer, vi återkommer till metoder för att lösa differentialekvationer i Ma5. Anledningen till att diffentialekvationer är intressanta är att nästan all naturvetenskaplig modellering slutar i någon form av differentialekvation.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Differentialekvationer och matematiska modeller (130-131)
Här finns olika exempel på tillämpade problemställningar. Som ni ser dyker differentialekvationerna upp i alla möjliga sammanhang!
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
3.4 Integraler
Integraler och primitiva funktioner (sid 134-137)
Från tidigare vet ni att en primitiv funktion brukar betecknas med versal. Exempelvis $F(x)$ har $f(x)$ som sin derivata, dvs. $F'(x)=f(x)$. Eftersom ni först fått lära er att derivera brukar det vara smidigt att helt enkelt "tänka baklänges".
"Funktionen jag söker skall bli det jag har om jag deriverar den sökta funktionen!"
Definition av integral
Integralen $A= \displaystyle \mathop {\lim }\limits_{n \to \infty } \sum\limits_{i = 1}^n {\Delta x} \cdot f({x_i}) = \displaystyle \int_a^b f(x) \text{d}x= \Big[ F(x) \Big]_a^b = F(b) - F(a)$ är ett tal
Om Riemannsumman och integralen. Lägg märke till hur Riemann Summan alltmer närmar sig integralens exakta värde i takt med att antalet segment $n$ ökas.
Förhållandet mellan den primitiva funktionen $F(x)$ och integralen av $f(x)$.
Experimentera med olika funktioner och notera speciellt att det alltså är funktionsvärdet till den primitiva funktionen $F(x)$ som motsvarar arean under kurvan $f(x)$ och x-axeln! Lek också med integrationsgränserna och se hur dessa påverkar integralens värde.
Bevis:
$\begin{aligned} F'(x)&=\displaystyle \lim_{h \rightarrow 0}\frac{F(x+h)-F(x)}{h} \\
&=\lim_{h \rightarrow 0}\frac{1}{h}\left ( \int_{a}^{x+h}f(t)dt-\int_{a}^{x} f(t)dt)\right )\\
&
=\lim_{h \rightarrow 0}\frac{1}{h}\int_{x}^{x+h}f(t)dt\\
&
=\lim_{h \rightarrow 0}f(c)=\lim_{c \rightarrow x}f(c)=f(x)\end{aligned}$
I första steget utnyttjas derivatans definition och i det andra definitionen av $F$ . I det tredje steget används räknelagar för integraler. I fjärde steget används medelvärdessatsen för integraler. I femte steget utnyttjas det faktum att $c$ ligger mellan $x$ och $x+h$, så då $h \rightarrow 0$ gäller att $c \rightarrow x$. Sista steget ges av att $f$ är kontinuerlig.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Grafiska metoder (138-141)
Som ni kunde se i GeoGebra konstruktionerna ovan kan arean under kurvor approximeras på flera olika sätt. Förutsättningen för att kunna beräkna integralens värde är att vi kan hitta en primitiv funktion till $f(x)$. Det är inte alltid givet att det går att hitta en sådan och då får man ta till approximativa metoder. Vilken metod som är bäst beror på funktionens utseende, ibland fungerar rektangelmetoden bäst och ibland kanske trapetsmetoden.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Areor mellan kurvor (142-145)
Arean mellan två kurvor $f$ och $g$ ges av integralen
$\int\limits_a^b {(f(x) - g(x))dx} $
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Integraler och areor (146-149)
Här undersöks hur integralen beräknas av en funktion som ligger både över och under x-axeln. Kom ihår att integralen i sig är ett tal, den kan däremot representeras av en area, men arean kan ju inte anta negativa värden. Så eftersom integralen av en funktion vars graf ligger under x-axeln är negativ måste vi manuellt ta bort minustecknet om vi vet att det handlar om den area.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Integraler och storheter (150-153)
I detta avsnitt visas hur användbart integralbegreppet är inom ett brett spektrum av discipliner.
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Sannolikhetsfördelning (154-158)
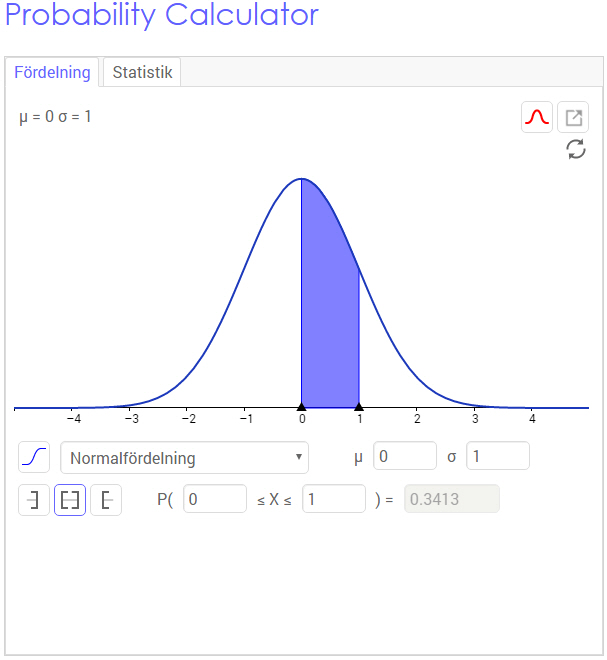
Normalfördelningen är ett exempel på en sannolikhetsfördelning, den är en viktig fördelning inom sannolikhetsteori och statistik. En normalfördelad variabel antar ofta värden som ligger nära medelvärdet $\mu$ och mycket sällan värden som har en stor avvikelse eller standardavvikelse $\sigma$, därav dess utseende.
Kurvans funktion kallas normalfördelningens täthetsfunktion $f(x)$ och det är en funktion som anger sannolikheten för att en variabel skall anta en visst värde.
$f(x)=\dfrac{1}{\sigma \sqrt{2 \pi}} \cdot e^{-\dfrac{(x-\mu)^2}{2\sigma^2}}$
En standardiserad normalfördelning har $\mu=0$ och $\sigma=1$. Dess täthetsfunktion kallas $\phi$ och ges av
$\phi(x)=\dfrac{1}{ \sqrt{2 \pi}} \cdot e^{-\dfrac{x^2}{2}}$
GeoGebra har i vanlig ordning en massa bra resurser. Här hittar ni en interaktiv Probability Calculator (Sannolikhets beräknare).
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
3.6 Rotationsvolymer
Skivmetoden (sid 165-170)
Integralberäkning kan också användas för att beräkna volymer av vissa symmetriska kroppar. Exakt samma princip som för beräkning av areor med hjälp av intregral kan användas. Dvs. att man skivar upp kroppen i det här fallet i små volymer och summerar dessa volymer över ett givet intervall. När antalet skivor ökar så minskar skivornas bredd mot noll och vi får en tvärsnittsarea. Det är funktionen för denna tvärsnittsarea som vi söker och som vi sedan integrerar över givet intervall, resultatet ges som volymen av rotationskroppen.
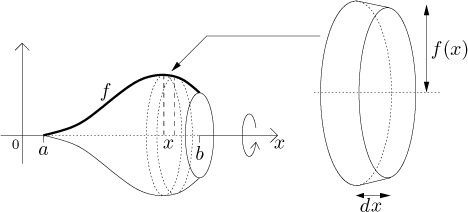
Vi kan dela upp skivmetoden i två delar. Antingen har vi rotation kring x-axeln eller rotation kring y-axeln. Vi får följande uttryck.
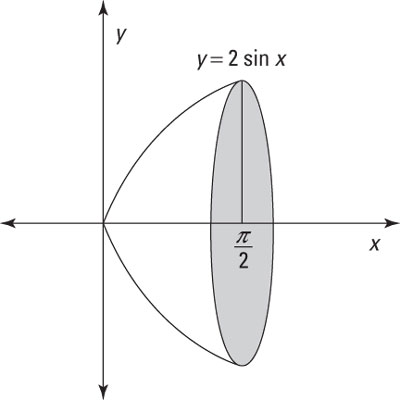
Rotation kring x-axeln |
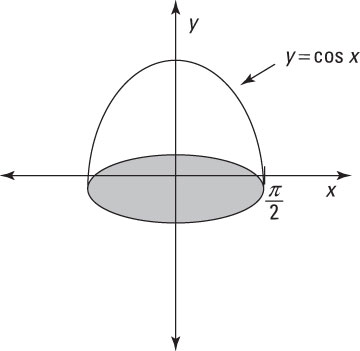
Rotation kring y-axeln |
|---|---|
$V= \displaystyle \int_{x=a}^{x=b}\pi y^2 \text{d}x$ |
$V= \displaystyle \int_{y=a}^{y=b}\pi x^2 \text{d}y$ |
 |
 |
| Övningsuppgifter sidan 17 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 101 | 102 | 103 | 104 | 105 | 106 | 107 | 108 | 109 | 110 |
| 111 | |||||||||
Blandade övningar med mera kapitel 3
| Testa dig själv sidan 193 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Blandade övningar 3 UTAN digitala hjälpmedel sidan 194 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Blandade övningar MED digitala hjälpmedel sidan 195 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | ||
Blandade övningar med mera kapitel 1-4
| Blandade övningar 1-3 UTAN digitala hjälpmedel sidan 196 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | ||||
| Blandade övningar 1-3 MED digitala hjälpmedel sidan 189 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| 37 | 38 | ||||||||