3.1 Medelhastighet och Momentanhastighet

3.1.1 Om medel- och momentanhastighet

Medelhastigheten är sträckan dividerat med tiden, dvs.

$\bar{v}=\dfrac{s}{t}$

SI-enheten för hastighet är meter per sekund, m/s.

Lek gärna med den här appen (klicka på bilden nedan), som på ett bra sätt illustrerar begreppen!

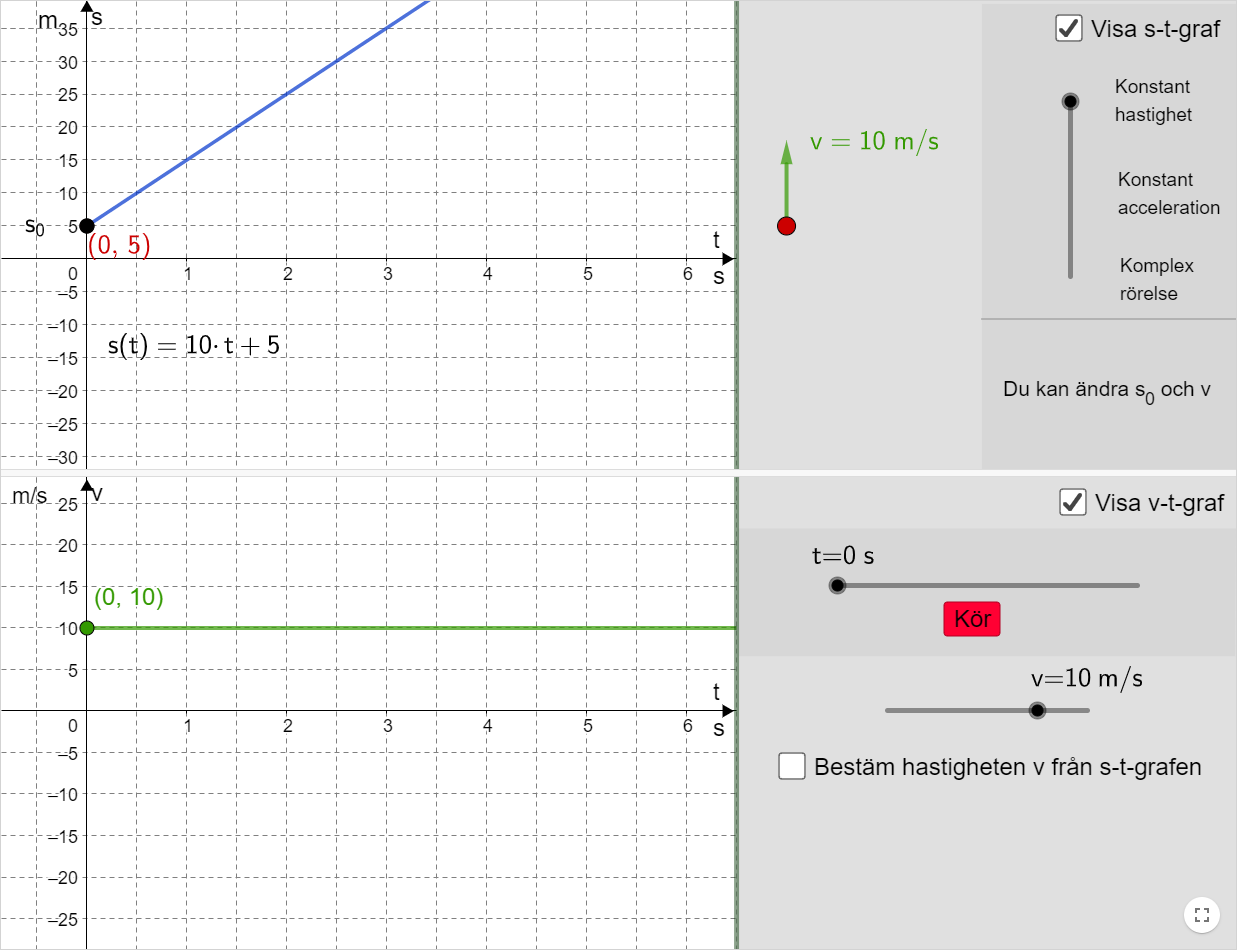Bil som rör sig med konstant acceleration. Man kan välja startpunkt, begynnelsehastighet och acceleration (glöm inte att trycka på ENTER efter att du matat in ett värde).

---

3.1.2 Hastighet som vektor

Storheter som har både storlek och riktning kallas för vektorer. Vektorer brukar symboliseras med pilar. Pilens längd anger storleken och pilens riktning anger vektorns riktning.

Övningsuppgifter sidan 50
301	302	303	304	305	306	307	308	309	310
311	312	313	314	315	316	317

---

3.1.2 Sträcka-tid-diagram

Hur avståndet förändras med tiden redovisas sedan i ett sträcka-tid-diagram (s-t-diagram). Man kan då lätt få en överblick över rörelsen.

Övningsuppgifter sidan 54
318	319	320	321	322	323	324	325	326

3.2 Acceleration

Precis som det låter är hastigheten konstant när den inte förändras.

Här finns några java-appar till som ni kan leka lite med.

Bil som rör sig med konstant acceleration. Man kan välja startpunkt, begynnelsehastighet och acceleration (glöm inte att trycka på ENTER efter att du matat in ett värde).

Inbromsning från konstant hastighet. Den gula bollen högst upp illustrerar först starthastigheten, i st- och vt-graferna är detta den gröna linjen. När du trycker på Bromsa (Brake) börjar inbromsningen av den gula bollen, det markeras med ett litet vitt streck högst upp och med rött i graferna! Prova lite olika värden och försök förutse vad som skall hända.

Övningsuppgifter sidan 60
327	328	329	330	331	332	333	334	335	336
337	338

3.3 Hastighet-tid-diagram

Momentanhastigheten är exempelvis den hastighet som bilens hastighetsmätare visar i varje ögonblick! Öva lite grand på att bestämma momentanhastigheten ur en graf. Det handlar om att bestämma lutningen för tangenten till grafen vid en viss tidpunkt. Finns beskrivet i boken på sidan 57.

3.3.1 Acceleration-tid-diagram

Övningsuppgifter sidan 69
339	340	341	342	343	344	345	346	347	348
349	350

3.4 Rörelse med konstant acceleration

När ett föremåls hastighet ändrar sig är rörelsen accelererad.

Acceleration:	Acceleration definieras som hastighetsändring under en viss tid. Accelerationen betecknas med $a$. Matematiskt samband $a=\dfrac{\Delta v}{\Delta t}$. Enheten för acceleration är (meter per sekund) per sekund, m/s$^2$.

Rörelseformlerna

Även här kan ni med fördel använda appen, som även illustrerar accelererad rörelse.

Hastighetsformeln vid konstant acceleration:	Vid konstant acceleration fås hastigheten som $v=v_0+at$, där $v_0$ är starthastigheten. Jämför $s_0$ i sträckformeln vid konstant hastighet, som ju där motsvaras av startläget.

Sträckformel 1:	När ett föremål har konstant acceleration, kan sträckan $s$ under tiden $t$ beräknas som $s=\bar{v}\cdot t=\dfrac{1}{2}\left(v_0+v\right)\cdot t$

Om man kombinerar Hastighetsformeln vid konstant acceleration med sträckformel 1 så får man sträckformel 2.

$s=\bar{v}\cdot t=\dfrac{1}{2}\left(v_0+\color{red}v\right)\cdot t=\dfrac{1}{2}\left(v_0+\color{red}{v_0+at}\right)\cdot t=v_0t + \dfrac{1}{2}at^2$

Sträckformel 2:	När ett föremål har konstant acceleration, kan sträckan $s$ under tiden $t$ också beräknas som $s=v_0t + \dfrac{1}{2}at^2$

Sambandet kan också illustreras med hjälp av areorna i en vt-graf, se nedan!

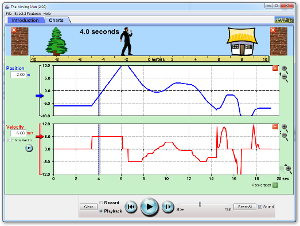
The Moving Man Kolla också in denna app och lek lite med den för att förstå begreppen. Man kan välja startpunkt, begynnelsehastighet och acceleration. Man kan också dra mannen manuellt. Det går också bra att mata in en godtycklig funktion $x(t)$ och sedan spela upp det.

Flera exempel på likformigt accelererad rörelse När du valt Edit v-t graph kan du skapa din egen likformiga accelererade rörelse genom att flytta på de röda punkterna. Du kan sedan spela upp rörelsen i slowmotion. Övning: Skapa din egen v-t graf så att s-t grafen har en max- och minpunkt ungefär som på bilden nedan. Svara sedan på följande frågor. Vid en viss tidpunkt $t_{max}$ har s-t grafen en maxpunkt. Vad betyder det för kroppens rörelse, och hur ser v-t grafen ut runt den punkten? Hur ser a-t grafen ut? Vad har v och a för tecken runt $t_{max}$? Gör samma sak för minpunkten $t_{min}$.

Övningsuppgifter sidan 77
350	351	352	353	354	355	356	357	358	359

★-UPPGIFTER

★-Uppgifter sidan 79
360	361	362	363	364	365	366	367	368	369
370	371	372	373	374

★★-Uppgifter sidan 81
375	376	377	378	379	380	381	382	383	384

★★★-Uppgifter sidan 83
385	386	387	388	389	390	391

Instuderingsfrågor

Instuderingsuppgifter kapitel 3