4.1 Newtons kraftlagar
4.1.1 Kraft (sid 88)
Krafter |
||
|---|---|---|
Storhet |
Beteckning |
Enhet |
Kraft |
F |
Newton (N) |
Definition |
|---|
1 N är den kraft som krävs för att accelerera ett föremål med massan 1 kg med 1 m/s$^2$ |
| F=m$\cdot$ a (kg\cdot m/s$^2$ = N) |
Kraftverkan |
|---|
En kraft kan förändra ett föremåls hastighet, form och rotation. Enheten för kraft är som sagt Newton (N). |
Han ansåg också att elementen söker sin "naturliga plats"! -Stenen faller till sin naturliga plats på jorden.
Med all naturlig rörelse menas att tingen söker sin naturliga plats.
Påtvingad rörelse däremot möter motstånd och det krävs en kraft utifrån. Aristoteles menade att ju snabbare ett föremål rör sig, desto större kraft måste verka på det. Konstant kraft skulle ge konstant hastighet och om kraften upphör så stannar föremålet.
Denna rörelselära verkade så vettig att den dominerade världsbilden i nästan 2$\,$000 år!
Galilei
Galileo Galilei formulerade två lagar som avvek från Aristoteles:
Galileis två lagar |
|---|
Om ingen kraft påverkar ett föremål i rörelse, så kommer det att fortsätta med konstant fart och riktning. |
Om nettokraften är konstant skild från 0, så kommer hastigheten att ändras. |
Newton
Isaac Newton är kanske den främste naturvetenskaplige forskaren genom tiderna. Han utvecklade nya matematiska metoder för att kunna formulera sina teorier om dynamiken (läran om kraft och rörelse) och gravitationen. Mer om Newton senare.
Avståndskrafter och kontaktkrafter
Avståndskrafter |
Kontaktkrafter |
|---|---|
Tyngdkraften |
Friktionskrafter |
Elektrisk kraft |
|
Magnetisk kraft |
Notera att även kontaktkrafter mikroskopiskt sätt är elektriska avståndskrafter!
Vektorer
Kraft är en vektorstorhet, vilket innebär att kraften har både storlek (den mäter vi i enheten Newton), men också en riktning (vanligtvis anges riktningen som en vinkel i förhållande till en koordinataxel).
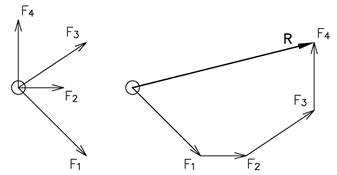
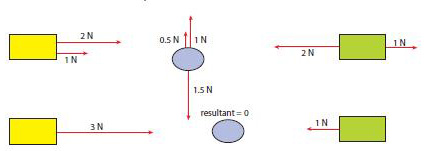
Resultantkraft
Resultantkraft |
|---|
Resultanten av två eller flera krafter är en tänkt kraft som har samma verkan som de verkliga krafterna har tillsammans.
|
Newtons nollte lag |
|---|
Resultanten av två likriktade krafter är lika med summan av krafterna. Resultanten av två motriktade krafter är lika med skillnaden mellan den största och den minsta kraften. Resultanten har samma riktning som den största kraften.
|
4.1.2 Newtons första lag (sid 92)
Isaac Newton är kanske den främste naturvetenskaplige forskaren genom tiderna. Han utvecklade nya matematiska metoder för att kunna formulera sina teorier om dynamiken (läran om kraft och rörelse) och gravitationen. Mer om Newton senare.
Newtons 1:a lag |
|---|
När resultanten av alla krafter som verkar på ett föremål är lika med noll, är föremålet i vila eller i rörelse med konstant hastighet. Med matematik: Om $F_{res}=0$, så är hastigheten $v$ konstant (OBS! Även $v=0$). eller omvänt Om $v$ är konstant (OBS! Även $v=0$), så är $F_{res}=0$. |
| Övningsuppgifter sidan 94 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 401 | 402 | 403 | 404 | 405 | 406 | ||||
4.1.3 Newtons andra lag (sid 95)
Isaac Newton är kanske den främste naturvetenskaplige forskaren genom tiderna. Han utvecklade nya matematiska metoder för att kunna formulera sina teorier om dynamiken (läran om kraft och rörelse) och gravitationen. Mer om Newton senare.
Newtons 2:a lag |
|---|
Resultantkraften är lika med massan multiplicerat med accelerationen. Med matematik: $F_{res}=m\cdot a$ |
Newtons 2:a lag igen (tänkbara formuleringar) |
|---|
Om ett föremål rör sig med konstant hastighet är den resulterande kraften på föremålet noll. Om den resulterande kraften på föremålet noll, rör sig föremålet med konstant hastighet. $F_{res}=0$ $\Longleftrightarrow$ $\vec{v}$ Om ett föremål påverkas av en resultantkraft ändras föremålets hastighet. Om ett föremåls hastighet ändras, påverkas det av en resultantkraft. Om ett föremål påverkas av en kraft, men dess hastighet förblir konstant, måste det finnas fler krafter. |
| Övningsuppgifter sidan 102 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 407 | 408 | 409 | 410 | 411 | 412 | 413 | |||
4.1.4 Newtons tredje lag (sid 99)
Isaac Newton är kanske den främste naturvetenskaplige forskaren genom tiderna. Han utvecklade nya matematiska metoder för att kunna formulera sina teorier om dynamiken (läran om kraft och rörelse) och gravitationen. Mer om Newton senare.
Newtons 3:a lag |
|---|
När två föremål verkar på varandra med krafter, är krafterna lika stora och motsatt riktade. Krafterna verkar längs samma räta linje. Alla krafter uppträder parvis och motriktade. Det finns ingen ensam kraft, för varje kraft som verkar på ett föremål finns en lika stor och motriktad kraft (någonstans). Ett tips för att hitta paret av ”kraft och motkraft”, eller ”aktionskraft och reaktionskraft” som de också kallas är: Aktions och reaktionskraften verkar inte på samma kropp. |
Det är vanligt att Newtons 3:e lag blandas ihop med den 1:a lagen. För att skilja dem åt så kom ihåg att den 3:e lagen handlar om två olika krafter som verkar på två olika föremål! Den första (och den andra) lagen handlar om flera krafter som verkar på ett och samma föremål.
Diverse exempel |
|
|---|---|
| Exempel 1 | |
Om tennisspelarens racket påverkar bollen med en kraft så påverkar bollen spelarens racket med en lika stor men motriktad reaktionskraft. |
 |
| Exempel 2 | |
Om jag trycker på ett häftstift mot en vägg med kraften 100 N... |
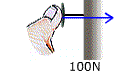 |
...så utövar häftstiftet en lika stor kraft på min tumme tillbaks. (det är den som gör ont) |
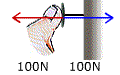 |
Samtidigt kan man säga att häftstiftet trycker mot väggen med kraften 100 N och väggen trycker tillbaks på häftstiftet med en lika stor kraft. |
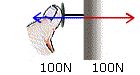 |
| Exempel 3 | |
| Var finns motkraften till tyngdkraften? |  |
Jorden påverkas av en lika stor kraft som du påverkas av den. |
 |
| Exempel 4 | |
| Mer om krafter och motkrafter! | |
Krafter som verkar på avstånd
Newton kunde inte beräkna storleken på konstanten $G$ i sin gravitationslag, men han visste att den var liten eftersom vi inte känner av några krafter från föremål/massor i vår närhet! Det var Henry Cavendish som långt senare genom experiment bestämde storleken på den universella gravitationskonstanten $G$, även om hans avsikt med sitt experimentet syftade till att mäta Jordens densitet!
| Övningsuppgifter sidan 102 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 414 | 415 | 416 | 417 | 418 | 419 | 420 | 421 | 422 | 423 |
4.2 Krafter i tillvaron
4.2.1 Tyngdkraft (sid 103)
4.2.2 Normalkraft (sid 107)
| Övningsuppgifter sidan 110 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 424 | 425 | 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 |
4.2.3 Gravitationskraft (sid 112)
Newtons Gravitationslag |
|---|
Krafterna mellan två kroppar är proportionella mot massorna och omvänt proportionella mot kvadraten på avståndet mellan dem. Med matematik: $F=G\dfrac{m_1m_2}{r^2}$, där $G=6.67\cdot 10^{-11}$ Nm$^2$/kg och $r$ är avståndet mellan de båda kropparnas centrum. |
4.2.4 Kraftfält (sid 114)
4.2.5 Hookes lag (sid 115)
4.2.6 Dynamometern (sid 118)
| Övningsuppgifter sidan 110 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 424 | 425 | 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 |
4.2.7 Friktion (sid 121)
4.2.8 Lutande plan (sid 124)
| Övningsuppgifter sidan 110 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 424 | 425 | 426 | 427 | 428 | 429 | 430 | 431 | 432 | 433 |
Kraftriktning och kraftens riktning
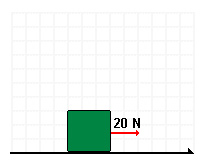
Riktningen på en kraft är alltid i förhållande till något annat, ofta ett koordinatsystem. Exempelvis, om vi definierat positiv x-axel som positiv riktning för våra krafter så skulle en kraft som pekar och verkar i motsatt riktning få ett minustecken framför sitt belopp.
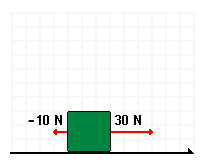
F$_{res}=30$N$+(−10$ N)$=30$ N$−10$ N$=20$ N
Kraftriktning då krafterna inte är parallella
Eftersom krafter är vektorer så kan resultanten av två krafter som inte är parallella lösas med hjälp av vektoraddion. Jag har gjort en GeoGebra applet nedan där ni grafiskt kan se hur resultanten bestäms av två godtyckliga vektorer (krafter).
Resultanter med GeoGebra-applet.
Vektorerna u och v, (vi kan tänka oss dem som krafter i detta fall) adderas till en resulterande kraft $F_r=u+v$. Det går att förändra vektorerna u och v genom att dra i respektive pilspets. Lägg märke till hur resultanten förändras både till storlek och riktning. Det smidiga skrivsättet för resultanten kallas matrisform, det är inget konstigt egentligen, men tillhör en matematik som normalt introduceras först på universitet och högskolenivå. Ni klurar säkert snabbt ut hur det fungerar!
Resultanter grafiskt med Java-applet.
En bra java-applet från Walter Fendt som illustrerar hur man grafiskt bestämmer resultanten till två eller flera krafter (maximalt 5 krafter i denna applet). Ange antalet krafter, dra i de blå kraftpilarna för att bestämma deras storlekar och riktningar!

Komposanter grafiskt med Java-applet.
En annan bra java-applet från Walter Fendt som illustrerar hur man grafiskt delar upp en kraft i två komposanter utmed godtyckliga riktningar. Dra först i kraftpilen och välj dess storlek och riktning, därefter ange riktningarna på de komposanter som du vill att kraften skall delas upp i!

★-UPPGIFTER
| ★-Uppgifter sidan 131 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 459 | 460 | 461 | 462 | 463 | 464 | 465 | 466 | 467 | 468 |
| 469 | 470 | ||||||||
| ★★-Uppgifter sidan 134 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 471 | 472 | 473 | 474 | 475 | 476 | 477 | 478 | 479 | 480 |
| 481 | 482 | ||||||||
| ★★★-Uppgifter sidan 44 | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| 483 | 484 | 485 | 486 | 487 | 488 | 489 | 490 | 491 | 492 |