9.1 Elektrisk laddning
Coulombs lag
Laddade partiklar påverkar varandra med elektriska krafter. Kraftens storlek beräknas med Coulombs lag.
| Coulombs lag | $F=k\dfrac{q_1q_2}{r^2} \textrm{, där } k=8.99\cdot 10^{9} \textrm{Nm}^2 \textrm{/C}^2$ |
|---|
Lös 9.01-9.06, 9.08 ev. (9.09)
9.2 Elektriska fält
Elektrisk fältstyrka är givet som kraft per laddning, mellan två metallplattor ges den elektriska fältstyrkan också som spänningen dividerat med avståndet mellan plattorna.
Homogent elektriskt fält, fältlinjerna ritas med jämna mellanrum!

| Elektrisk fältstyrka | $E=\dfrac{F}{q}=\dfrac{U}{s}$ |
|---|
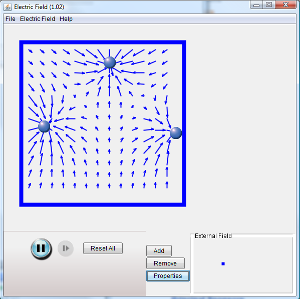
Denna applet simulerar ett elektriskt fält mellan laddade partiklar, det går att lägga till partiklar med godtycklig massa och laddning, Bra!
Mer om laddningar och fält! Lek lite med denna applet från PhET.
Lös 9.10-9.12
9.3 Spänning
Elementarladdningen
Lös 9.13-9.18, ev. (9.19,9.20)
9.4 Ström
Mätning av ström och spänning
Lös 9.21-9.26
9.5 Resistans
Ohms lag
Resistansen i en metalltråd
Supraledning
Lös 9.27-9.33
9.6 Koppling av motstånd
Seriekoppling
Parallellkoppling
Lös 9.34-9.37, ev. (9.38-9.41)
9.7 Potential
Kirchhoffs lagar
Lös 9.42-9.47
9.8 Elektrisk energi och effekt
Elektrisk effekt
Den effekt som en elektrisk komponent utvecklar bestäms av sambandet P = U · I P = effekten och mäts i watt [W], U = spänningen över komponenten, I = strömmen genom komponenten. Då Ohms lag ( U = R · I ) gäller kan U ersättas med R·I P = U · I = R·I · I = R I² Strömmen I kan ersättas med U/R (Ohms lag) vilket ger P = U · I = U · U/R = U² / R Energiutvecklingen E i en elektrisk komponent = Effekt · tid. E = P · t Energi kan då skrivas E = P · t = U · I · t eller E = U²/ R · t eller E = R I² · t